CQL by Example — Part II

This is the second part of the main line of the CQL by Example document suite.

Let us state up front that we haven't a clue what we're doing. We're just groping around hoping to get lucky. When we go looking for patterns in solution trees with scores of variations with their threats and blocks and duals and cooks and patterns expressed across phases, we're in unexplored territory. According to the online reference, the language was never intended to go where we're going. So there you have it. Beyond this line there be dragons.

What we can promise is an entertaining ride, whether we ultimately arrive at our destination or not. What destination? CQL in the problem domain. The grand experiment. On the other side of that broad and treacherous sea.¹

Examples in the problem domain

Each of the examples to follow will match at least a handful of problems in one or more of the problem databases found on the project site. The full solution trees have been generated using the Scid++ solving facility, translating Popeye solutions to native format.

We should mention that we've extended the CQL header to include two pseudo-parameters:

The nolinearize parameter turns off linearization for the line filter.
The alwayscomment parameter disables smart comments so that we can tag each variation matched by a line filter with a comment.

The Scid++ CQL search facility strips the parameters out of the CQL header and converts them to their respective command line switches before launching the CQL sub-process.

With regard to the alwayscomment parameter, Lewis Stiller points out one potential problem area and a solution:

One issue with using -alwayscomment is that it will not work if you wanted to comment every move in your line, with say different comments (as is done, say, in turton.cql).

The general way to handle the issue of commenting every variation, but also deriving the benefit of smart comments, is to wrap the line in an echo, and modify the final filter of the line only to match if its current position equals the target of the echo, e.g.:
echo (source target) {
  mate // limit target to mate here for efficiency
  source:line // evaluate the line at the source, making sure it ends at target
    --> move primary comment ("first ply")
    --> Checker = move to . from [qrb] secondary comment ("second ply")
    --> check and move to between(Checker K) primary comment ("third ply")
    --> {currentposition==target  mate  comment("CrossCheck")}
}

Direct play

Cat description...

The thematic cross-check
Generally speaking, the cross-check is a tactic in which one side blocks a check by interposition and gives check with the same move. In the case of a compositional theme, the cross-check typically gives mate by discovery.
We can have any number of different flavors of this theme. We'll first demonstrate a query matching the generic pattern and then we'll give a couple of queries designed to match a very specific cross-check pattern.

// The thematic cross-check - generic.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

ccCount = 0
line  // Count the number of cross-checks by interposition.
  --> move primary  // the key
  --> Checker =? move to . from [qrb]  // must be a line piece giving check
  --> check and move to between(Checker K)  // the interposition gives...
  --> {mate  ccCount += 1  comment("CrossCheck")}  // ... mate by discovery

actualCount = 0
line  // Count the total number of lines in actual play.
  --> move primary --> not move null --> move primary
  --> mate and actualCount+=1

// A lower bound on thematic play and thematic play outweighs byplay.
ccCount >= 4  and  actualCount < ccCount * 3 / 2

Note that the mate is necessarily by discovery, else the interposing [and presumably mating] piece could be captured.

Next we'll consider a cross-check theme wherein Black gives check leaving a [previously guarded] mating candidate unguarded (either by abandoning the guard or by interfering with the guard). White answers by interposing a piece, mating by discovery with the [now] unguarded piece.

// The thematic cross-check - abandoning the guard.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

Count = 0
line
  --> move primary  // the key
  --> {
        // The set of mating aspirants with a threatened discovery in place.
        Maters =? ray diagonal (k A B) | ray orthogonal (k A R)
        // The guards of the mating aspirants.
        Guards =? a attacks Maters
        // Every mating aspirant is guarded.
        Maters > 2 and square all Mater in Maters {Guards attacks Mater}
        // The line piece giving the first check.
        Checker =? move to . from [qrb]
      }
  --> {
        check
        // At least one mating candidate is no longer guarded.
        Unguardeds =? square Mater in Maters {not Guards attacks Mater}
        // The interposing piece moves to block the check.
        move to between(Checker K)
      }
  --> {
        mate
        // Mate is by discovery and is by our now unguarded aspirant.
        Unguardeds & ((A & ~move to . previous) attacks k)
        Count += 1  comment("CrossCheck")
      }
Count > 2

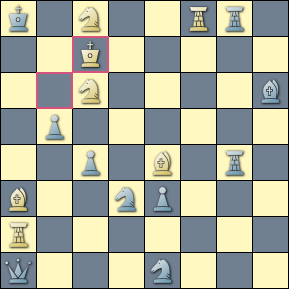We establish a lower bound on the number of matching lines and on the number of mating candidates, which are criteria for a more interesting composition.
The query matches a problem by Davidenko (Shakhmaty v SSSR - 1986), where the guard of the mating piece is sometimes abandoned and sometimes interfered with. We give a slice of the solution tree showing the cross-checks in actual play following the key.

                      ┌ -- ──── Nb6#
                      ├ Qg7+ ── Be7# CrossCheck
                      ├ Qe5+ ── Bd6# CrossCheck
       ┌ Kc7! threat ─┤
       │              ├ R4g7+ ─ N6e7# CrossCheck
       │              ├ Bf4+ ── Ne5# CrossCheck
       │              └ R8g7+ ─ N8e7# CrossCheck

Finally, we'll search for a cross-check theme with a knight wheel at the crux. Certain aspects of thematic play get twisted about with this pattern. The initial check by black is necessarily by discovery (though it could be a double check), with the knight repeatedly clearing the same line. And the cross-check by white is not [necessarily] by interposition.
It should surprise no one that a fully-wheeled cross-check theme is either very rare or perhaps has never been composed (we can't find one). Thus, we search for [a range of] partial wheels with each knight move leading to a cross-check with mate, and where every white response is unique.

// The thematic cross-check - with wheeling knight.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

line
  --> move primary  // the key
  --> { // actual play
        Actual = currentposition
        // Eliminate from consideration any actual play with duals.
        not find {terminal and (depth > parent:depth and
                    not parent:move null previous)}
        // Iterate over every black knight on the board.
        piece Knight in n {
          Moves = 0 // Count the total number of knight moves.
          // Match a range of wheels, where each knight move has a
          // unique white response.
          Found = find 4 8 {
            terminal
            // The previous position is given by a knight move with check.
            parent:{check
                    move from Knight previous
                    comment("Knight at " parent:Knight)}
            Moves += 1
            // Is the knight move followed by a unique white response?
            not echo(source target) {
              terminal and ancestor(Actual currentposition)
              parent:move from Knight previous
              // Only the knight move is different... disqualifying.
              ~(source & target) == 2
            } // echo
            comment("CrossCheck")
          } // find
          // All knight moves have a unique white response.
          Found == Moves
        } // piece
      } // compound

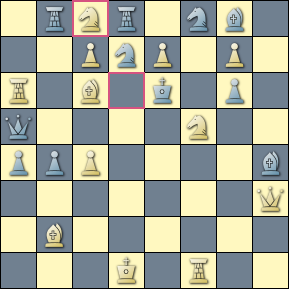We eliminate solutions with duals just to make our counting job easier (threat lines with duals being irrelevant). And the use of the echo filter is, perhaps, not the most efficient allocation of CPU cycles, but it feels more natural in detecting changes in board position.
The query matches a problem by Thorsson (Torneo Olímpico - 1936), in which promotion play also shows up in the thematic pattern. The diagram depicts the board after the key move.

                     ┌ -- ──────────────── Bd5#
                     ├ Kf7 ─────────────── Nfd6#
                     ├ Nb6+ Knight at d7 ─ cxd8=N# CrossCheck
       ┌ Nc8! threat ┼ Nc5+ Knight at d7 ─ Nfd6# CrossCheck
       │             ├ Ne5+ Knight at d7 ─ Nd4# CrossCheck
       │             ├ Nf6+ Knight at d7 ─ exd8=N# CrossCheck
       │             └ Rb6 ─────────────── cxd8=N#
       ├ Bd5+? ─────── Qxd5+!
       │             ┌ Qxd8 ────────────── Bd5#
       ├ cxd8=N+? ───┤
       │             └ Rxd8!
 Start ┤
       │             ┌ Be7 ─────────────── Qxe7#
       ├ e8=Q+? ─────┤
       │             └ Rxe8!
       │             ┌ Be7 ─────────────── Rxe7#
       ├ e8=R+? ─────┤
       │             └ Rxe8!
       │             ┌ Qxc7 ────────────── Bd5#
       │             ├ Qb6 ─────────────── Bd5#
       │             ├ Qxa6 ────────────── Bd5#
       └ -- ─────────┤
                     │                   ┌ Bxd5#
                     ├ Qd5+ ─────────────┤
                     │                   └ cxd5#
                     └ Rb6 ─────────────── cxd8=N#

The thematic self-block
The key move forces black to block flight squares in the king's field, perhaps eliminating the immediate threat but allowing an alternate or a set mate. The self-block may be of an outright flight square or of a square previously guarded by the mating piece.

// The thematic self-block.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

Count = 0
line
    --> move primary  // the key
    --> {
        // Eliminate from consideration any actual play with duals.
        not find {terminal and (depth > parent:depth and
                    not parent:move null previous)}
        // A friendly moves adjacent to the king in actual play.
        Flight =? move to (. attackedby k) from ~k  comment("SelfBlock")
        }
    --> {
        piece Mater = move from .
        // Either the block is of an outright flight square or the
        // block is of a square previously guarded by the mating piece. 
        parent:{move from k to Flight legal or Mater attacks Flight}
        // The mating move is not a capture of the blocking piece.
        not move from Mater capture Flight
        Count += 1
        }
Count >= 6

We narrow the matching problems to those with at least six self-blocks in the solution. Note that we need not terminate the line of play, as we've already established that the problem is mate-in-2.
The query matches a composition by Fleck (Nepszava - 1939), which was awarded 1st prize in the competition.

Inspecting the solution, we can see that the key's threat also covers both of the black king's flights, adding to the fun. And that even the other white queen on the board gets some action. Nice.

                      ┌ -- ────────────── Qxd5#
                      ├ Rxc5 SelfBlock ── Rxe4#
                      ├ Rdxe5 SelfBlock ─ Qc4#
                      ├ Rgxe5 SelfBlock ─ Be3#
       ┌ g8=Q! threat ┤
       │              ├ Rxg8 ──────────── Rxd5#
       │              ├ dxe5 SelfBlock ── Ne6#
       │              ├ dxc5 SelfBlock ── Nc6#
       │              └ Nxc5 SelfBlock ── Qb2#
       ├ Ne6+? ──────── Kxe5!
       ├ Rxe4+? ─────── Kxc5!
 Start ┼ Rxd5+? ─────── Rxd5!
       ├ Nc6+? ──────── Kxc5!
       │              ┌ Rxc5 ──────────── Rxe4#
       │              ├ Rgxe5 ─────────── Be3#
       │              ├ Rxg7 ──────────── Rxd5#
       │              ├ Rg6 ───────────── Rxd5#
       └ -- ──────────┼ dxe5 ──────────── Ne6#
                      ├ dxc5 ──────────── Nc6#
                      ├ f5 ────────────── Rxd5#
                      ├ fxe5 ──────────── Ne6#
                      └ Nxc5 ──────────── Qb2#

The thematic self-pin
It's not unusual to find a self-pin in a solution, but it is fairly rare to encounter a problem with the self-pin as the theme. The query is simple and to the point, with the king stepping into the pin followed by the mating piece moving into the attack field of the pinned piece.

// The thematic self-pin.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

Count = 0
line
    --> move primary  // the key
    --> {
        // Eliminate from consideration any actual play with duals.
        not find {terminal and (depth > parent:depth and
                    not parent:move null previous)}
        // The king moves into the pin.
        move from k to ~k  comment("SelfPin")
        }
    --> {
        // The mating piece is attacked by the pinned piece.
        move to (. attackedby (pin through a))
        Count += 1
        }
Count >= 4

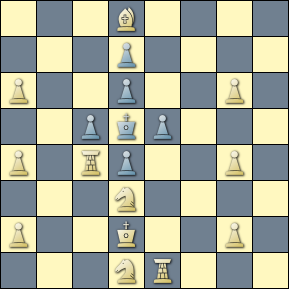The pin filter with a leading through parameter yields a set representing the square(s) occupied by the pinned piece(s). The mating piece must move onto a square that is attacked by one off those pieces.
Also note that the expression — stipulating that the king moves into the pin — at the same time guards against matching a null move (which is technically a move by the king).

The query matches a composition by Allison (Manchester Guardian - 1953) that is not exactly a great challenge to the solver. But it does have a certain charm and elegance about it, given the symmetry in the position and in the solution, which, by the way, also qualifies as a starflight.

                     ┌ Kxc4 SelfPin ─ Ne3#
                     ├ Kxe4 SelfPin ─ Nc3#
       ┌ Re4! block ─┤
       │             ├ Ke6 SelfPin ── Nf4#
       │             └ Kc6 SelfPin ── Nb4#
       │             ┌ Ke6 ────────── Nf4#
       ├ N1b2? block ┼ Kc6 ────────── Nb4#
       │             └ e4!
 Start ┤
       │             ┌ Kxc4 ───────── N1b2#
       ├ Rxe5+? ─────┼ Kc6 ────────── Nb4#
       │             └ dxe5!
       │             ┌ Ke6 ────────── Nf4#
       ├ Rxc5+? ─────┤
       │             └ dxc5!
       │             ┌ Ke6 ────────── Nf4#
       └ -- ─────────┤
                     └ Kc6 ────────── Nb4#

The starflight theme
The key to this pattern of play is typically a blocking move, forcing the opposing king to step into each of his diagonal flight squares (actual play), where mate is to follow. Being most interested in pure thematic play, we eliminate from consideration any solutions with byplay.

// The starflight theme.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

line
  --> move primary  // the key
  --> currentposition:{
        // The king moves to all four diagonal flights.
        (move to (diagonal 1 k) from k  comment("Flight")) == 4
        // The king makes only those four moves.
        (move to ~k from k) == 4
        // Only the king makes a move.
        not move from ~k
        // All mates are by the same knight.
        //N == 1 and not find {terminal  k attackedby ~N}
      }

We disable linearization to allow for a tallying of all the moves emanating from the one position.
The composition by Hartong (The Observer - 1920) is fairly typical of the starflight. Again, we have a board with some appealing symmetry and a key that is within reach of the novice.

The solution tree has been sliced to eliminate virtual play.

                    ┌ Kd4 Flight ─ Nf3#
                    ├ Kf4 Flight ─ Bc7#
       ┌ Ba5! block ┤
       │            ├ Kf6 Flight ─ Bc3#
       │            └ Kd6 Flight ─ e5#
       ⁓
       │
 Start ┼
       │
       ⁓
       │            ┌ Kd4 ──────── Nf3#
       │            ├ Kf4 ──────── Nd3#
       └ -- ────────┤
                    ├ Kf6 ──────── Bc3#
                    └ Kd6 ──────── Bg3#

Uncomment the last line of the second constituent of the line filter to match what might strike one as an unlikely pattern. And, in fact, the pattern is rare and the matching problems all derive of the same idea.

Unpinned and unleashed
We rarely see a composition with multiple serial pins in the starting position, but there are a few. The problem is usually a block, with black [usually] forced to interpose a piece in each of its own pins, allowing the unpinned white piece to mate. Of course, the serial pin prevents the black pinning piece from capturing the pinned white piece, which would be bad form in any event.
We'll search for problems with at least two serial pins, each of which is broken, with the unpinned piece moving to mate. Matching problems are sorted by the number of serial pins.

// Unpinned and unleashed.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

Pinned =? pin through A
serialPins =? pin through (pin from a)

sort "Serial count" serialPins >= 2
comment("White pinned at:" Pinned " Black pinned at:" serialPins)

line
  --> move primary from ~(K|Pinned)  // the key
  --> {
      hascomment "block"
      // All of the pinned pieces get their shot at mate.
      piece all Piece in Pinned
        find all {terminal  Piece attacks k  comment("Unleashed")}
      }

We stipulate that the key may not be by the king (breaking the pins) or by one of the pinned white pieces. The latter stipulation is something of an artificial requirement imposed by the semantics of the piece filter. The set over which the piece filter iterates is a set of squares, not a set of pieces. If there is no piece on a square when the filter is evaluated, we'll get some unintended results.
The composition by Carra (8th American Chess Congress - 1921) has three serial pins (White pinned at:[b5,c6,d7] Black pinned at:[b4,e4,f7]) and a blocking key.

                      ┌ Qxa4 ── Nxd6# Unleashed
                      ├ d5 ──── Qxc5# Unleashed
       ┌ a3! block ───┤
       │              ├ Nb6 ─── Nxd6# Unleashed
       │              └ Nc7 ─── Nb6# Unleashed
       ⁓
       │
 Start ┤
       │
       ⁓
       │              ┌ d5 ──── Qxc5#
       │              │       ┌ Na3#
       └ -- ──────────┼ Nb6 ──┤
                      │       └ Nxd6#
                      └ Nc7 ─── Nb6#

Thematic self-interference
The key presents a threat. In answer to that threat, every defense amounts to interference with a friendly's ability to interpose the mate. We look for solutions having the number of interfering lines within a given range, and then sort the matching problems by that number.

// Thematic self-interference.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

Start = currentposition
Terms = 0
line
  --> move primary // the key
  --> {
      hascomment "threat"
      sort "Interfering lines"
        {find 4 100 {
          // Ignore the threat line.
          terminal and not parent:move null previous
          Terms += 1
          Mater = A attacks k
          Interferer = parent:{move to . previous}
          // Check each line piece for interference with the defense
          // of the king.
          piece Piece in ([qrb] & ~Interferer) {
            // Get the square on which the piece might have interposed.
            Interpose = Start:{between(Mater k) attackedby Piece}
            // Has the piece been interfered with?
            ray(Piece Interferer Interpose)
            comment("Interference of " Piece " at " Interferer)
          } // piece
        }} == Terms
      } // compound

To better understand the query, it probably helps to work backwards from the ray filter. From the terminal position, we're looking for the alignment of three squares: 1) the square occupied by the piece that has been interfered with, 2) the square occupied by the interfering piece, and 3) the square on which the mate might have been interposed, but for the interference.

We obtain these squares by examining three different positions. The squares for items one and two are trivial. They are the candidates for the interferee and the interferer. Item three requires some explanation. We cannot determine the would-be interposing square until we know the mating square. We can only know the mating square from the terminal position, but we can only know that a line piece might have interposed (but for the interference) from the starting position. The interferee must have had a clear line of attack intersecting with the mating line of attack from that position.

So, from the terminal position we acquire the mating square (Mater = A attacks k) and determine that from the starting position the interference candidate (bound to the Piece variable) had a clear line of attack to an interposing square (Start:{between(Mater k) attackedby Piece}). Then, if the candidates for the Interferee, the Interferer, and the Interposition are all aligned (ray(Piece Interferer Interpose)), we have our match.

Note that if we stipulate that the number of positions matched by the find filter is equal to the number of terminal positions, we have effectively eliminated solutions with byplay.

The composition by Golubev (Moscú-Leningrad - 1933) depicted in the diagram takes the theme of interference well beyond the search criteria given above. We just stumbled onto a little bonus.

                     ┌ -- ──── Nf7#
                     ├ Ne4 ─── Qe3# Interference of rb4 at e4
       ┌ Qd4! threat ┼ Bxd4 ── Rg3# Interference of rb4 at d4
       │             ├ Rxd4 ── Be7# Interference of bc3 at d4
       │             └ e5 ──── Qd8# Interference of bc3 at e5
       │             ┌ Rf4 ─── Qxf4#
       ├ Qxd2+? ─────┤
       │             └ Bxd2!
       ├ Qd8+? ─────── Bf6!
 Start ┼ Qe7+? ─────── Bf6!
       │                     ┌ Qxe6#
       │             ┌ Kf6 ──┤
       ├ Nf7+? ──────┤       └ Qd8#
       │             └ Kf4!
       │             ┌ Bd4 ─── Rg3#
       │             │       ┌ Qe7#
       │             ├ Rd4 ──┤
       └ -- ─────────┤       └ Be7#
                     │       ┌ Qd8#
                     └ e5 ───┤
                             └ Qe7#

The four corner block
Following a blocking key, at least four of the defenses in actual play are met by a mating move to a corner, and each of the four corners is covered. The mating piece is not necessarily the piece in the corner.
We're tempted to take a brute force approach to the query, which leaves us something short of being esthetically pleased. Repetitive, unimaginative and ugly.

// The four corner block.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

line
  --> move primary // the key
  --> hascomment "block" and
      {
      find { terminal and move to a1 previous }
      find { terminal and move to a8 previous }
      find { terminal and move to h1 previous }
      find { terminal and move to h8 previous }
      }

Reducing the four find invocations to one, we're feeling better about things. But...

// The four corner block.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

line
  --> move primary // the key
  --> hascomment "block" and
      find 4 {terminal  move to [a1,a8,h1,h8] previous}

... there's a problem. The move filter allows any number of matches to any or all of the squares given, which would only accidentally match a solution with moves to all four.
What we want is to find four matches where each of the four moves is to a unique corner. We borrow an idea from an online example to achieve our ends, maintaining a record of corner squares found and ensuring that any tested square is unique.

// The four corner block.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

// From two-piece-cycle.cql.
function Unique(Square Set) {
  not Square in Set  
  Set = Square | Set // insert Square into Set 
} 

Corners = ~.  // the empty set
line
  --> move primary // the key
  --> hascomment "block" and
      find 4 {
        terminal
        Unique(move to [a1,a8,h1,h8] previous  Corners)
        comment("Corner")
      }
Corners == 4  // superfluous test

Note that we can measure the number of unique corner squares by either of two methods: 1) as a range given for the find filter, or 2) as a measure of the cardinality of the Corners set. Either measure is sufficient by itself.
The composition by Kuznetsov (64 Shakhmatnoe obozrenie - 1996) was awarded an special honorable mention, with a solution that realizes the four corner theme as a starflight.

                     ┌ Kc4 ─── Na1# Corner
                     ├ Kxe4 ── Qh1# Corner
       ┌ Rg5! block ─┼ Kxe6 ── Bh8# Corner
       │             │       ┌ a8=Q# Corner
       │             └ Kxc6 ─┤
       │                     └ a8=B#
       │                     ┌ a8=Q#
       │             ┌ Kxc6 ─┤
       ├ Na1+? ──────┤       └ a8=B#
       │             └ Kxe4!
       │             ┌ Kc4 ─── Na1#
       │             ├ Kxe4 ── Qh1#
 Start ┤             │
       ├ Rf6? block ─┤       ┌ a8=Q#
       │             ├ Kxc6 ─┤
       │             │       └ a8=B#
       │             └ g5!
       │             ┌ Kc4 ─── Na1#
       │             │       ┌ a8=Q#
       ├ Qxg6? block ┼ Kxc6 ─┤
       │             │       └ a8=B#
       │             └ Kxe4!
       │             ┌ Kc4 ─── Na1#
       └ -- ─────────┤       ┌ a8=Q#
                     └ Kxc6 ─┤
                             └ a8=B#

The mutate
TBD: a work in progress... still a mess.
A block in which the key changes one or more of the set mates for a given defense. The following query matches a total mutate, where all of the set mates are changed. Matching games are sorted by the number of mutates.

Nested interphase traversal...

// The mutate.
cql(quiet variations alwayscomment)
initial  wtm  result 1-0  player black "#2"

// Compare two moves.
function SameMove(X Y) {
  X:{move from . previous} == Y:{move from . previous}
  X:{move to . previous} == Y:{move to . previous}
  // Account for promotions.
  X:{type move to . previous} == Y:{type move to . previous}
}

line
  --> move primary  // actual play
  --> {
        hascomment "block" and Actual = currentposition
        not find {terminal and depth > parent:depth}  // no duals
        Lines = find all {terminal}  // count the lines
        currentposition:{Defenders = move from a}  // the defending pieces
      }
Defenders > Lines / 2   comment("Defenders:" Defenders)

Abort = 0
line
  --> move null  // set play
  --> 4 <= sort "Mutate lines" {
        not find {terminal and depth > parent:depth}  // no duals
        // For every line in set play...
        find all {
          terminal  comment("id:" positionid)
          T = currentposition
          // ... find a mutate in actual play.
          if not Actual:find {
            terminal
            // For a given defense...
            SameMove(parent T:parent)
            // ... the mating moves differ.
            not SameMove(currentposition T)
            // The terminal positions differ.
            currentposition & T != .
            comment("Mutate:" T:positionid)
          } then Abort = 1
        } // find all
      } == Lines <= 8  // the compound returns the last evaluated filter
Abort == 0

Especially with a block, the black line pieces tend to consume a large percentage of the play, visiting every possible square in their field of attack and with the same white mating response. We can filter out those solutions fairly reliably with a simple measure of the percentage of the defending moves that are made by a unique defending piece. We get a quick count of the number of unique defenders with linearization disabled (currentposition:{Defenders = move from a}), then require that they represent at least half of the defending lines (Defenders > Lines / 2).
The Abort flag gives us an indication that some line(s) in set play did not have corresponding mutate(s) in actual play. Since we can't actually abort the outer traversal, we set an artificial switch to indicate that we would have if we could have. While there are other ways of achieving the same end, this may be the clearest.

Every line in actaul play represents a mutate. Range is given on the compound filter, which retuurns the result given by the last filter of the compound. Could as easily have given the range as parameters to the find all filter, but as given we receive a bit of an insight into the language.

Finally, stipulating that the terminal positions differ eliminates the following scenario. The problem is a complete block. The key move is by the mating piece and is a waiting move. For any given defense, the mating piece moves to the same square as in set play. Thus, the mating moves differ, but the terminal positions are identical. Technically, such changed play qualifies as a mutate. Esthetically, not so much.

The matching composition by Fleck (Magyar Sakkvilag - 1943) was awarded an Honorable Mention (not for the total mutate). All eight set mates are changed in actual play. The full solution reveals a Stocchi theme expressed across three phases.

                    ┌ Nxh2 ─ Nfg3# Mutate:20
                    ├ Ng3 ── Nfxg3# Mutate:22
                    ├ Ne3 ── Nfg3# Mutate:24
                    ├ Nd2 ── Nfg3# Mutate:26
       ┌ Nf5! block ┤
       │            ├ d2 ─── Qc2# Mutate:28
       │            ├ g3 ─── f3# Mutate:30
       │            ├ exd4 ─ Qxd4# Mutate:32
       │            └ e6 ─── Nxd6# Mutate:34
       ⁓
       │
 Start ┤
       │
       ⁓
       │            ┌ Nxh2 ─ Ng3# id:20
       │            ├ Ng3 ── Nxg3# id:22
       │            ├ Nxe3 ─ Ng3# id:24
       │            ├ Nd2 ── Ng3# id:26
       └ -- ────────┤
                    ├ d2 ─── Bc2# id:28
                    ├ g3 ─── Bf3# id:30
                    ├ exd4 ─ Rxe7# id:32
                    └ e6 ─── Nf6# id:34

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

The Holst theme
TBD: a work in progress... still a mess.

cql (variations alwayscomment quiet)
initial
Purity = 0
player black ~~ "^#(\d).*" and StipDepth = int \1
Key=--(primary  currentposition)
//Key:{path focus p (--=▲) {3,}}
local dictionary TTries
path keepallbest
  -- secondary and not nullmove //and originalcomment "block"
     Try=∙
     Key:{path  keepallbest
         -- *
         -- Try:{pieceid to} == pieceid to  and
            Try:{type to} == type to  and
            Try:{to} == to and
            parent:{currentmove --=▲}  IdP=∙  IdL=IdP
            Try:{
               --=▲(originalcomment "$1")
               path  keepallbest
                 (-- not originalcomment "$1"  IdC=∙
                     IdP:{Found=find{
                           IdC:{pieceid to} == pieceid to and
                           IdC:(to) == to and
                           distance(IdP ∙) == distance(Try IdC)
                           comment("(match)")
                           }
                         ancestor(IdL Found)  IdL=Found
                         }
                     if mate or Found:mate 
                       Try:{comment("(thematic)")}
                 ) {2,}
                 TTries[IdP] = Try  //message(IdP ":" Try)
               } // Try
     } // Key

#TTries >= 1

Key:{
  LCount = 0
  find all {
    terminal
    FCount = find all <-- TTries[∙]
    if LCount < FCount then LCount = FCount
  }
  find all {
    terminal
    if LCount == 1
      then find <-- {
             TTries[∙]
             parent:{piece T = to  TS = to  TT = typename to}
             TTries[∙]:{
               T--=▲(originalcomment "$1")
               not T--TS=TT(originalcomment "$1")
               if Purity > 0
                 countmoves --=▲(originalcomment "$1") ==
                 countmoves --(originalcomment "$1")
             }
           }
    if LCount == find all <-- TTries[∙]
      then find all <-- TTries[∙] and comment("(thematic)")
  }
}

//LCount == 1

Especially with a block,
The matching composition by

                    ┌ Nxh2 ─ Nfg3# Mutate:20
                    ├ Ng3 ── Nfxg3# Mutate:22
                    ├ Ne3 ── Nfg3# Mutate:24
                    ├ Nd2 ── Nfg3# Mutate:26
       ┌ Nf5! block ┤
       │            ├ d2 ─── Qc2# Mutate:28
       │            ├ g3 ─── f3# Mutate:30
       │            ├ exd4 ─ Qxd4# Mutate:32
       │            └ e6 ─── Nxd6# Mutate:34
       ⁓
       │
 Start ┤
       │
       ⁓
       │            ┌ Nxh2 ─ Ng3# id:20
       │            ├ Ng3 ── Nxg3# id:22
       │            ├ Nxe3 ─ Ng3# id:24
       │            ├ Nd2 ── Ng3# id:26
       └ -- ────────┤
                    ├ d2 ─── Bc2# id:28
                    ├ g3 ─── Bf3# id:30
                    ├ exd4 ─ Rxe7# id:32
                    └ e6 ─── Nf6# id:34

Help play

Cat description...

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Self/Reflex play

Cat description...

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Example template
Explanation...
```
cql() true
```

Credits

The diagrams appearing in this document were created with the Scid vs PC application's board screenshot facility. The piece set is included with that application and is credited on the project's site.

Footnotes

¹ We're having alot of fun with more than just the one language.

CQL by Example — Part II

Examples in the problem domain

Direct play

Help play

Self/Reflex play

See also

Credits

Footnotes

Content