Game Tree Traversal in a CQL Universe
This document (still under development) is a companion to the CQL by Example document presented on the Scid++ project site. As we graduate from the relatively straight-forward searches in the conventional domain to the more challenging queries in the problem domain, we require a solid understanding of the structure of the game tree and of the language techniques for traversing the tree.
We are now in the business of matching compositional themes expressed across variations (branches of the tree) in the line of play. In representing the various phases of a solution, the game tree can become quite large and complex. The material that follows sets about to demonstrate techniques for isolating those phases, for identifying relationships between the nodes of the tree, and for matching patterns in the play.
A review of the game tree
The first order of business is to establish a clear understanding of the terminology used in referring to the game tree. The online CQL documentation includes a couple of relevant introductory sections: 1) a review of the formal structure of the game tree, and 2) an explanation of how the current position is managed as the CQL engine steps through the game tree. Throughout this document we will employ the same terminology as is used in those reference sections. We'll also expand on that terminology to include the notion of an inner and an outer traversal of the tree.
For any given query, traversals of the game tree may be many and may be nested to an arbitrary depth. An outer traversal of the tree takes place as the engine visits each node in the tree in a prescribed order in the course of query evaluation. If the variations parameter is given in the CQL header, the outer traversal visits each node for variations as well as for the mainline.
Within the context of the outer traversal, inner (nested) traversals may take place as a function of a particular CQL filter having traversing capabilities: namely, the find, line, and echo filters. The inner traversals may be intraphase or interphase or may span the entire solution tree.
The position operator allows for the evaluation of a [compound] filter in the context of an arbitrary position. The operator is typically employed in matching interphase patterns or themes in the course of an inner traversal, as is demonstrated in several of the examples below. We should clarify one point in particular with regard to the operator. The position filter (left of the operator) may be (and usually is) a position variable, in which case the variable is evaluated as true if it holds a valid position id. It matters not at all that the evaluation takes place in the context of the current position, whereas the variable assignment may have taken place in a different context.
The PGN standard looks on a chess game as a structured collection of moves. CQL, on the other hand, views the game as a tree structure in which every node represents a position. Each position, then, is associated with a move (or moves) leading to the next position(s). It's largely a matter of emphasis, but with consequences that can lead to a great deal of head-scratching.
When a move filter matches a position, by default it matches the position from which the move was made. With [potentially] multiple moves emanating from any one position, one might match any or all of them and still match only the one position. So how does one distinguish between moves in a complex game tree laden with scores of branches? By matching the positions to which the moves are made, i.e., the positions resulting from the moves. With the variations parameter given in the CQL header, the move previous filter (move filter with the previous parameter) is typically the flavor of choice. Several examples are given below.
Examples of game tree traversal
Our aim with the examples that follow is to demonstrate some of the essential language techniques employed in the traversal of a game tree, in the course of constructing a CQL query specific to the problem domain. We'll first cover the basics of node recovery and tree traversal, and we'll then give a few examples of the application of those techniques.
The queries have been tested against one or more of the project's support problem databases, with solutions generated by the Scid++ problem solving extension. Those solutions adopt a consistent phase structure of the game tree with some relevant problem-specific metadata registered with each problem's PGN header.
[Event "American Chess Nuts"] [Site "EduSadier Direct Mate in Two"] [Date "1858.??.??"] [Round "80854"] [White "LOYD Samuel"] [Black "#2 -- Actual+Virtual+Set Play"] [Result "1-0"] [Stipulation "#2"] [Solver "Popeye v4.85"] [FEN "5b2/1p2p1p1/1Q1pR1P1/6P1/k2p1K1p/1p1N3P/r1n3P1/nN1B4 w - - 0 1"]
The structure of the solution tree has the key move in the mainline, followed by virtual play and finally by set play. For helpmates the solution(s) lead the way, trailed by set play if present. Set play and virtual play are appropriately tagged with leading PGN comments.
Any given move that is a threat or a block is labeled as such, and conventions are observed for the use of NAGs in solutions. The '!' NAG identifies both the key move and a refutation to a try, while the '?' NAG identifies the try. Note that a '--' sequence in the game tree represents a null move, most commonly found 1) at the root of set play, and 2) in primary play following a threat.
One need not stare for very long at a PGN-formatted solution tree with hundreds (thousands) of nodes to begin to feel a serious headache coming on. The PGN representation of the tree can be virtually unreadable. We'll employ an alternative presentation format that is much less a threat to our health, rendering the typically broad and shallow solution in a vertical orientation. (The tree rendering extension is implemented on the project's utility branch.)
The basics
Before we get into the fine detail of tree traversal, we should introduce a few techniques for identifying positions of interest, selected lines of play, solution phases, and classes of problem in the orthodox domain. Filtering may be based on metadata, on node properties, or on characteristics of the solution tree. The examples that follow assume that the problem database has been solved by the Scid++ solving extension.
- Class filtering
-
In constructing a query in the problem domain, we will commonly wish to filter a database based on the class of a problem. For a database with a mix of orthodox problems, we have just a few classes to choose from (direct/help/self/reflex), each with a distinctive set of identifying characteristics.
We can lump self and reflex mates into a single class for the sake of filtering, giving us just three qualifying sets of filters separating out the problems in the database.
// Direct mate. cql() initial wtm result 1-0
// Help mate. cql() initial btm result 1-0
// Self/reflex mate. cql() initial wtm result 0-1
-
Simply put, it is sufficient to give 1) side-to-move from the starting position, and 2) side-to-mate as a result, to deliver the three way distinction.
Stalemates are slightly more involved, as we need to further distinguish between the direct and self/reflex classes beyond the commonly held result, since both are white-to-move from the starting position. As it happens, we have a property of the solution tree for either class that will help to separate them out; namely, the side-to-move at the terminal position.
// Direct stalemate. cql() initial wtm find {stalemate btm}// Help stalemate. cql() initial btm result 1/2-1/2
// Self/reflex stalemate. cql() initial wtm find {stalemate wtm}-
In CQL-land, a stalemate filter yields the equivalent of a drawn result. For that matter, the mate and stalemate filters joined with side-to-move at the terminal position may substitute for the result filter in most circumstances. One approach employs metadata; the other relies on certain properties of the solution tree.
We should probably also take into account the white-to-move helpmate (e.g., H#3.5), which is technically indistinguishable from the direct mate in terms of qualifying characteristics that we can glean from the game tree. We'll need to turn to metadata to make that distinction.
By convention — for all databases that have been solved by the Scid++ solving extension — the PGN Black tag carries metadata which includes the problem's stipulation. CQL can match strings against any of the PGN tags in the standard seven tag roster. Thus, we can very easily filter for problems with a specific stipulation, or even a particular substring of the stipulation.
cql() player black "H#3.5"
-
One might well wonder why we don't simply turn to the player tag for all of our class filtering. But CQL only provides for substring matching on metadata, and has no text-based globbing or regular expression facilities (see the line filter for position-based). So if we wish to search on a range of particulars within a class of problem, we must resort back to properties of the game tree.
Update: With the release of version 6.1 of the language, we have a very well done string implementation with nicely integrated regular expressions. A regex may be applied to any PGN header tag, giving us ample flexibility in distinguishing classes of composition.
For example, suppose we're interested in finding all white-to-move help mates or help stalemates with a stipulation length that lies within a specific range. Then matching substrings in metadata just doesn't get the job done.
cql(quiet) initial wtm player black ".5" find {terminal btm mate or stalemate 5 < ply < 11}-
The player filter narrows the search down to the white-to-move flavor of a helpmate. Then we look for a solution tree with a terminal position at mate or stalemate and with ply at that terminal position within a given range. The query above will match all helpmates with stipulations in the range 'H[#=][3-4].5'.
Before moving on beyond class filtering, we should point out that at times it may be inconvenient or even downright impractical to filter problems by class on the fly by anchoring the outer traversal at the starting position. One should consider whether it might be simpler to execute two passes on the database, the first to filter on the class and the second to match on the query-proper, where an inner traversal might not even be necessary.
- Phase recovery
-
We can isolate each of the phases of a solution — matching the root position of the respective branch of the tree — by identifying the unique characteristics of the phase's move emanating from the starting position. That is, the key and subsequent actual play may be recovered as the primary move from the initial position. Likewise, virtual and set play are recovered as secondary play from the starting position.
First, we'll take a look at the wrong way of achieving our end.
cql(quiet variations) initial wtm result 1-0 move primary comment("(Key)") move to ~K secondary comment("(Try)") move null secondary comment("(Set)")-
Note that move to ~K amounts to a fictitious move not null, given that the definition of a null move is as "a move by the king of the side to move from and to the same square."
The query appears to match all of the correct nodes, tagging the positions with their respective comments as expected. But we have fallen victim to a slightly misleading artifact of a comment filter associated with a move filter, in that the comment does not tag the matching position. In fact, the query matches only the initial position on all three counts of the move filter.
1. Kc2 $1 {threat (Key)} ( {try} 1. Ne4+ $2 {(Try)} 1. ... Kb1 ( 1. ... Rxe5 $1 ) 2. Nd2# ) ( {set} 1. -- {(Set)} 1. ... R1g2 2. N1e2# ( 2. Nd3# ) ( 2. N1a2# ) ) 1. ... -- ( 1. ... R1g2+ 2. N1e2# ) ( 1. ... Bf5+ 2. Ne4# ) ( 1. ... bxc3 2. Bxc3# ) ( 1. ... R5g2+ 2. N3e2# ) 2. Nb3# 1-0 ┌ -- ──── Nb3# ├ R1g2+ ─ N1e2# ┌ Kc2! threat (Key) ┼ Bf5+ ── Ne4# │ ├ bxc3 ── Bxc3# │ └ R5g2+ ─ N3e2# Start ┤ │ ┌ Kb1 ─── Nd2# ├ Ne4+? (Try) ──────┤ │ └ Rxe5! │ ┌ N1e2# └ -- (Set) ────────── R1g2 ─┼ Nd3# └ N1a2#-
What we have, then, is a query that tells us only that a matching direct-mate has a solution that includes all three phases of play. If we wish to match and acquire the positions at the root of the respective branches, we must identify the move that is made from the starting position and that leads to the root position.
cql(quiet variations) initial wtm result 1-0 find all { ply == 1 move primary previous and comment("(Key)") or move secondary previous and hascomment "$2" and comment("(Try)") or move null secondary previous and comment("(Set)") }-
The inner traversal anchors at positions with ply of one, and while the filters comprising a typical compound filter are joined by an implied logical and, here we employ a logical or operation so that we can match each of the roots as the outer traversal is anchored at the starting position. Note that we utilize the hascomment filter as an alternative distinguishing criteria in matching virtual play. Note also that we disassociate the comment filters from the move filters by interjecting an explicit logical and, thereby commenting the actual matching position.
A special case of phase recovery entails the isolation of cooks. One might wish to eliminate from consideration any solution that is cooked (of which there are thousands in a typical problem database), or one might wish to specifically target intentionally cooked solutions (e.g., Vlagsma (Probleemblad - 1978)).
The following snippet identifies every key position of a solution — including cooks — while employing just the outer traversal.
cql(quiet variations) ply == 1 and hascomment "$1"
- On the other hand, we can identify all problems with a cook and eliminate them from consideration.
cql(quiet variations) not find {ply == 1 move secondary previous hascomment "$1"}- For helpmates, we have a simpler recovery task as we have only the solution(s) and set play to distinguish. That is, we have set play and anything else that is not set play. Since (by convention) we have no NAGs to assist us in identifying the solution(s), we'll adopt precisely those complementary criteria.
cql(quiet variations) initial btm result 1-0 find all { ply == 1 move null secondary previous and comment("(Set)") or not move null secondary previous and comment("(Solution)") }- For a helpmate with two solutions and a single line in set play, the engine returns the following:
1. ... h1=R {(Solution)} ( 1. ... h1=B {(Solution)} 2. Nf3 Bg2 3. Ne5 Bb7 4. Nc6 Ba6 5. Na7# ) ( {set} 1. ... -- {(Set)} 2. Nf3 h1=B 3. Ne5 Bb7 4. Nc6 Ba6 5. Na7# ) 2. Kb2 Kxa4 3. Ne2 Rb1+ 4. Ka2 Rb4 5. Nc3# 1-0 ┌ h1=R (Solution) ─ Kb2 ─ Kxa4 ─ Ne2 ─ Rb1+ ─ Ka2 ─ Rb4 ─ Nc3# Start ┼ h1=B (Solution) ─ Nf3 ─ Bg2 ── Ne5 ─ Bb7 ── Nc6 ─ Ba6 ─ Na7# └ -- (Set) ──────── Nf3 ─ h1=B ─ Ne5 ─ Bb7 ── Nc6 ─ Ba6 ─ Na7#
- Threats and blocks
- A threat or a block may occur anywhere in actual play or in virtual play and is tagged with an appropriate comment by the Scid++ solving extension. Positions so tagged will match a hascomment filter with the corresponding argument.
cql(quiet variations) hascomment "threat" and comment("(Threat)") or hascomment "block" and comment("(Block)")- A threat is followed in the primary line of play by a null move and then by the threatened line of play.
1. e8=R $1 {block (Block)} ( {try} 1. e8=Q $2 {block (Block)} 1. ... Kf6 ( 1. ... f6 $1 ) 2. Kg4 {threat (Threat)} 2. ... -- ( 2. ... Kg7 3. Kf5# ) 3. Bb2# ) 1. ... Kf6 ( 1. ... f6 2. Re3 {block (Block)} 2. ... Kg5 3. Re5# ) 2. Kg4 {threat (Threat)} 2. ... -- ( 2. ... Kg7 3. Kf5# ) 3. Bb2# 1-0 ┌ -- ── Bb2# ┌ Kf6 ─ Kg4 threat (Threat) ┤ ┌ e8=R! block (Block) ┤ └ Kg7 ─ Kf5# │ └ f6 ── Re3 block (Block) ─── Kg5 ─ Re5# Start ┤ │ ┌ -- ── Bb2# │ ┌ Kf6 ─ Kg4 threat (Threat) ┤ └ e8=Q? block (Block) ┤ └ Kg7 ─ Kf5# └ f6!
- The refutation
- By convention, the refutation of a try in virtual play is tagged with a NAG of '$1'. Refutations will be found at a terminal position, of course, and in a line (primary or secondary) immediately following the try.
cql(quiet variations) terminal hascomment "$1" and comment("(Refute)")1. Qd3 $1 {block} ( {try} 1. Nf3+ $2 Ke4 $1 {(Refute)} ) ( {try} 1. Qb8 $2 {block} 1. ... Kd5 ( 1. ... f4 $1 {(Refute)} ) 2. Qb5# ) ( {try} 1. Qb5+ $2 Rd5 $1 {(Refute)} ) ( {try} 1. Qg3+ $2 f4 ( 1. ... Kd5 $1 {(Refute)} ) 2. Qg5# ) ( {try} 1. Qf3 $2 {threat} 1. ... -- ( 1. ... f4 2. Qh5# ( 2. Qe4# ) ) ( 1. ... Rc6 $1 {(Refute)} ) 2. Nc4# ) ( {try} 1. Qe3+ $2 Kd5 $1 {(Refute)} ) 1. ... Kd5 ( 1. ... f4 2. Qe4# ) ( 1. ... Rd5 2. Nc4# ) ( 1. ... Ra6 2. Qxd4# ) ( 1. ... Rb6 2. Qxd4# ) ( 1. ... Rc6 2. Qxd4# ) 2. Qb5# 1-0 ┌ Kd5 ─────────── Qb5# ├ f4 ──────────── Qe4# ├ Rd5 ─────────── Nc4# ┌ Qd3! block ─┤ │ ├ Ra6 ─────────── Qxd4# │ ├ Rb6 ─────────── Qxd4# │ └ Rc6 ─────────── Qxd4# ├ Nf3+? ─────── Ke4! (Refute) │ ┌ Kd5 ─────────── Qb5# ├ Qb8? block ─┤ Start ┤ └ f4! (Refute) ├ Qb5+? ─────── Rd5! (Refute) │ ┌ f4 ──────────── Qg5# ├ Qg3+? ──────┤ │ └ Kd5! (Refute) │ ┌ -- ──────────── Nc4# │ │ ┌ Qh5# ├ Qf3? threat ┼ f4 ───────────┤ │ │ └ Qe4# │ └ Rc6! (Refute) └ Qe3+? ─────── Kd5! (Refute)
- The null move
- Following the convention established by the Scid++ solving extension, a null move either will establish the root node for set play or will follow a threat in the primary line of play. The primary/secondary test will reliably distinguish between the two contexts, whereas the mainline/variation test will not.
cql(quiet variations) move null previous and comment("(Null)") if move previous primary then comment("(Primary)") else comment("(Secondary)")1. Kc2 $1 {threat} ( {try} 1. Ne4+ $2 Kb1 ( 1. ... Rxe5 $1 ) 2. Nd2# ) ( {set} 1. -- {(Null) (Secondary)} 1. ... R1g2 2. N1e2# ( 2. Nd3# ) ( 2. N1a2# ) ) 1. ... -- {(Null) (Primary)} ( 1. ... R1g2+ 2. N1e2# ) ( 1. ... Bf5+ 2. Ne4# ) ( 1. ... bxc3 2. Bxc3# ) ( 1. ... R5g2+ 2. N3e2# ) 2. Nb3# 1-0 ┌ -- (Null) (Primary) ─ Nb3# ├ R1g2+ ─────────────── N1e2# ┌ Kc2! threat ──────────┼ Bf5+ ──────────────── Ne4# │ ├ bxc3 ──────────────── Bxc3# │ └ R5g2+ ─────────────── N3e2# Start ┤ │ ┌ Kb1 ───────────────── Nd2# ├ Ne4+? ────────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- (Null) (Secondary) ─ R1g2 ───────────────┼ Nd3# └ N1a2#
- Lines of play
- Every node in the game tree is either in the mainline or in a variation, and is either in a primary line of play or a secondary line of play. Every position in the mainline is necessarily in a primary line of play, but a position that is in a variation might also be in a primary line of play.
cql(quiet variations) mainline and comment("(M)") or variation and comment("(V" depth ")") move primary previous and comment("(P)") or move secondary previous and comment("(S)")- It is the move previous filter that gives us the move leading to the current position. Note that even a null move is in one or the other of the lines of play.
1. Kc2 $1 {threat (M) (P)} ( {try} 1. Ne4+ $2 {(V1) (S)} 1. ... Kb1 {(V1) (P)} ( 1. ... Rxe5 $1 {(V2) (S)} ) 2. Nd2# {(V1) (P)} ) ( {set} 1. -- {(V1) (S)} 1. ... R1g2 {(V1) (P)} 2. N1e2# {(V1) (P)} ( 2. Nd3# {(V2) (S)} ) ( 2. N1a2# {(V2) (S)} ) ) 1. ... -- {(M) (P)} ( 1. ... R1g2+ {(V1) (S)} 2. N1e2# {(V1) (P)} ) ( 1. ... Bf5+ {(V1) (S)} 2. Ne4# {(V1) (P)} ) ( 1. ... bxc3 {(V1) (S)} 2. Bxc3# {(V1) (P)} ) ( 1. ... R5g2+ {(V1) (S)} 2. N3e2# {(V1) (P)} ) 2. Nb3# {(M) (P)} 1-0 ┌ -- (M) (P) ───── Nb3# (M) (P) ├ R1g2+ (V1) (S) ─ N1e2# (V1) (P) ┌ Kc2! threat (M) (P) ┼ Bf5+ (V1) (S) ── Ne4# (V1) (P) │ ├ bxc3 (V1) (S) ── Bxc3# (V1) (P) │ └ R5g2+ (V1) (S) ─ N3e2# (V1) (P) Start ┤ │ ┌ Kb1 (V1) (P) ─── Nd2# (V1) (P) ├ Ne4+? (V1) (S) ─────┤ │ └ Rxe5! (V2) (S) │ ┌ N1e2# (V1) (P) └ -- (V1) (S) ───────── R1g2 (V1) (P) ─┼ Nd3# (V2) (S) └ N1a2# (V2) (S)
The inner filters
CQL includes a number of filters that provide for an inner or nested traversal of the game tree. That nesting can actually take place to an arbitrary depth with, for example, a line filter given as a constituent of another line filter.
When nesting traversals, one can look on the leading qualifying filters of the outer traversal as establishing an anchor from which to conduct the inner traversal. If there are no anchoring filters, then every node in the tree becomes an anchor point. The anchor will, of course, be established by a filter that matches the anchored position. The inner traversal may take place over the entire tree, over just the branch rooted by the anchor, or over an entirely different branch (i.e., solution phase).
In demonstrating the mechanics of the various filters, we'll employ the comment and message filters as an assist in visualizing the inner and outer traversals of the tree. And to eliminate excess noise in the tree, we'll tag only the anchor point for the outer traversal even though that traversal might walk the entire tree.
But before we get to the filters, we should probably demonstrate the outer traversal of the tree as a reference point for the inner traversals.
- With the variations parameter given in the CQL header the engine visits each node in the game tree, evaluating the main body of the query at every position.
cql(quiet variations) comment("position " positionid) message("position " positionid)- The comment filter evaluates as true for every position. The result returned by the engine reveals the ordering of the nodes of the tree.
┌ -- position 2 ───── Nb3# position 3 ├ R1g2+ position 4 ── N1e2# position 5 ┌ Kc2! threat position 1 ┼ Bf5+ position 6 ─── Ne4# position 7 │ ├ bxc3 position 8 ─── Bxc3# position 9 │ └ R5g2+ position 10 ─ N3e2# position 11 Start ┤ │ ┌ Kb1 position 13 ─── Nd2# position 14 ├ Ne4+? position 12 ─────┤ │ └ Rxe5! position 15 │ ┌ N1e2# position 18 └ -- position 16 ───────── R1g2 position 17 ─┼ Nd3# position 19 └ N1a2# position 20- Likewise, the message filter evaluates as true for each node and shows that the outer traversal walks the tree in the same order as id's are assigned. Position 0 is the starting position.
Game: 1 move 1(wtm): position 0 Game: 1 move 1(btm): position 1 Game: 1 move 2(wtm): position 2 Game: 1 move 2(btm): position 3 Game: 1 move 2(wtm)[4]: position 4 Game: 1 move 2(btm)[5]: position 5 Game: 1 move 2(wtm)[6]: position 6 Game: 1 move 2(btm)[7]: position 7 Game: 1 move 2(wtm)[8]: position 8 Game: 1 move 2(btm)[9]: position 9 Game: 1 move 2(wtm)[10]: position 10 Game: 1 move 2(btm)[11]: position 11 Game: 1 move 1(btm)[12]: position 12 Game: 1 move 2(wtm)[13]: position 13 Game: 1 move 2(btm)[14]: position 14 Game: 1 move 2(wtm)[15]: position 15 Game: 1 move 1(btm)[16]: position 16 Game: 1 move 2(wtm)[17]: position 17 Game: 1 move 2(btm)[18]: position 18 Game: 1 move 2(btm)[19]: position 19 Game: 1 move 2(btm)[20]: position 20
- The find filter
- From the starting position, the find all filter traverses the game tree in an order identical to that of the outer traversal. The initial filter anchors us at that starting position for the execution of the inner traversal.
cql(quiet variations) initial find all {comment("find " positionid)}┌ -- find 2 ───── Nb3# find 3 ├ R1g2+ find 4 ── N1e2# find 5 ┌ Kc2! threat find 1 ┼ Bf5+ find 6 ─── Ne4# find 7 │ ├ bxc3 find 8 ─── Bxc3# find 9 │ └ R5g2+ find 10 ─ N3e2# find 11 Start ┤ │ ┌ Kb1 find 13 ─── Nd2# find 14 ├ Ne4+? find 12 ─────┤ │ └ Rxe5! find 15 │ ┌ N1e2# find 18 └ -- find 16 ───────── R1g2 find 17 ─┼ Nd3# find 19 └ N1a2# find 20- The next query anchors us at the root of set play rather than at the starting position, with the inner traversal covering that entire branch of the tree. Note that the inner traversal includes the current position.
cql(quiet variations) move null previous secondary and comment("outer " positionid) find all {comment("inner " positionid)}┌ -- ──────────── Nb3# ├ R1g2+ ───────── N1e2# ┌ Kc2! threat ─────────┼ Bf5+ ────────── Ne4# │ ├ bxc3 ────────── Bxc3# │ └ R5g2+ ───────── N3e2# Start ┤ │ ┌ Kb1 ─────────── Nd2# ├ Ne4+? ───────────────┤ │ └ Rxe5! │ ┌ N1e2# inner 18 └ -- outer 16 inner 16 ─ R1g2 inner 17 ┼ Nd3# inner 19 └ N1a2# inner 20-
The reference for the find filter suggests that the filter traverses all "future" positions from the current position, which is at best ambiguous in a variations context. One could be forgiven for reading that definition to mean that the filter will traverse all positions with a position id that is greater than the position id of the current position, which would be incorrect.
More precisely, the filter will traverse all positions for which the current position is an ancestor; that is, all positions in the tree having the current position at the [possibly distant] root of the visited node's branch. For example:
cql(quiet variations) ply == 1 move to ~K secondary previous and comment("outer " positionid) find all {comment("inner " positionid)}┌ -- ───────────── Nb3# ├ R1g2+ ────────── N1e2# ┌ Kc2! threat ────────────┼ Bf5+ ─────────── Ne4# │ ├ bxc3 ─────────── Bxc3# │ └ R5g2+ ────────── N3e2# Start ┤ │ ┌ Kb1 inner 13 ─── Nd2# inner 14 ├ Ne4+? outer 12 inner 12 ┤ │ └ Rxe5! inner 15 │ ┌ N1e2# └ -- ────────────────────── R1g2 ──────────┼ Nd3# └ N1a2#
- The line filter
- As is the case with the find filter, a special case of the line filter — from the starting position and with a single constituent with a repetition factor — traverses the game tree in an order identical to that of the outer traversal.
cql(quiet variations alwayscomment) initial line --> {comment("line " positionid)}{*}┌ -- line 2 ───── Nb3# line 3 ├ R1g2+ line 4 ── N1e2# line 5 ┌ Kc2! threat line 1 ┼ Bf5+ line 6 ─── Ne4# line 7 │ ├ bxc3 line 8 ─── Bxc3# line 9 │ └ R5g2+ line 10 ─ N3e2# line 11 Start ┤ │ ┌ Kb1 line 13 ─── Nd2# line 14 ├ Ne4+? line 12 ─────┤ │ └ Rxe5! line 15 │ ┌ N1e2# line 18 └ -- line 16 ───────── R1g2 line 17 ─┼ Nd3# line 19 └ N1a2# line 20- The following query establishes an anchor at the root of every phase in virtual play, then traverses every descendant of the root. The lone constituent of the line filter is somewhat contrived in order to demonstrate the scope of the inner traversal. One should keep in mind, though, that in general the filter will only traverse however many nodes are necessary to determine that a particular line of play matches (or fails to match) each of its constituents, and each line is considered independently.
cql(quiet variations alwayscomment) hascomment "$2" and comment("outer " positionid) line --> {comment("inner " positionid)}{*}┌ -- ────────────── Nf6# ├ Rxc3 ──────────── Qxd4# ┌ Bb6! threat ───────────────────┤ │ ├ Rxe4 ──────────── Qc5# │ └ Nxb6+ ─────────── Nxb6# │ ┌ Qxd4# inner 12 │ ┌ -- inner 11 ────┤ │ │ └ Rxd4# inner 13 ├ Rxd3? threat outer 10 inner 10 ┼ Rxd3 inner 14 ─── Qxd3# inner 15 │ ├ Nb6+ inner 16 ─── Nxb6# inner 17 │ └ Kxc4+! inner 18 │ ┌ -- inner 20 ───── Ne3# inner 21 Start ┼ Qxd3? threat outer 19 inner 19 ┼ Nb6+ inner 22 ─── Nxb6# inner 23 │ └ Rxd3! inner 24 ├ Nb6+? outer 25 inner 25 ──────── Nxb6+! inner 26 ├ Nf6+? outer 27 inner 27 ──────── Kc5+! inner 28 │ ┌ -- inner 30 ───── Nf6# inner 31 │ ├ Rxe4 inner 32 ─── Qc5# inner 33 ├ Bd6? threat outer 29 inner 29 ─┤ │ ├ Nb6+ inner 34 ─── Nxb6# inner 35 │ └ Rxc3! inner 36 │ ┌ Rxc4 ──────────── Nf6# └ -- ────────────────────────────┼ Nb6+ ──────────── Nxb6# └ Nxc7 ──────────── Nb6#- Alternately, we can establish the "anchor" with the first constituent of the line filter, which is evaluated at the current position as the outer traversal visits each node. Technically, this "anchor" is established as part of the inner traversal. The option of taking this approach is largely a matter of taste.
cql(quiet variations alwayscomment) line --> hascomment "$2" and comment("anchor " positionid) --> {comment("repeat " positionid)}{*}┌ -- ────────────── Nb3# ├ R1g2+ ─────────── N1e2# ┌ Kc2! threat ────┼ Bf5+ ──────────── Ne4# │ ├ bxc3 ──────────── Bxc3# │ └ R5g2+ ─────────── N3e2# Start ┤ │ ┌ Kb1 repeat 13 ─── Nd2# repeat 14 ├ Ne4+? anchor 12 ┤ │ └ Rxe5! repeat 15 │ ┌ N1e2# └ -- ────────────── R1g2 ───────────┼ Nd3# └ N1a2#-
Keep in mind that with the line filter some lines of play may fail to match every constituent while others may satisfy the given criteria. Only one matching line of play in the branch is necessary for the filter to match the current [anchored] position.
At this point, it's reasonable to ask whether an inner filter is even necessary for simple queries. After all, the outer traversal walks the tree in the same fashion as a line filter anchored to the starting position (having a single repeating constituent that always matches).The answer to the question is... yes and no.
Taking the following seriously-contrived query as a starting point and executing it against our favorite solution tree, we can see that the lines matched are both in actual play. Note that we have a preamble that limits matching games to the direct-mate-in-2 class, and that the outer traversal is anchored at the initial position.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> move primary // the key --> currentposition: {move to [f5,c3,b1,e5] comment("Match")} == 2 and comment("Found")- Ignore the currentposition filter and the position operator for the moment. They merely disable linearization on the second constituent of the line filter so that the move filter can match multiple moves from the one position.
┌ -- ───────── Nb3# ├ R1g2+ ────── N1e2# ┌ Kc2! threat Found ┼ Bf5+ Match ─ Ne4# │ ├ bxc3 Match ─ Bxc3# │ └ R5g2+ ────── N3e2# Start ┤ │ ┌ Kb1 ──────── Nd2# ├ Ne4+? ────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ──────────────── R1g2 ──────┼ Nd3# └ N1a2#-
With the line filter, the first constituent pins us to the position following the key such that all matching lines will have the key in the line. If we are to employ the outer traversal, instead, we must (actually, the imperative is a bit too strong but let's not go off on any tangents) free up the CQL engine to evaluate the body at every position in the tree. That is, the initial filter must go out the window.
But we still need to stipulate that the problem has white-to-move at the initial position, as part of the preamble filtering by class. Since we can no longer anchor the outer traversal at that position, what to do? The position operator allows us to test for white-to-move at position 0, the starting position, without anchoring the outer traversal.
cql(quiet variations) position 0:wtm result 1-0 player black "#2"
- With adjustments to the preamble in place, we'll give the move filter exactly as it appears in the line filter, but now standing alone in the main body of the query. As given, the filter will be evaluated at every node in the tree.
cql(quiet variations) position 0:wtm result 1-0 player black "#2" {move to [f5,c3,b1,e5] comment("Match")} == 2 and comment("Found")-
Note that linearization is not an issue outside of a line filter.
The result returned by the engine shows that we matched four lines, two in actual play and two in virtual play. Not quite what we were hoping for. The "line" is not anchored in actual play as it was with the line filter.
┌ -- ────────── Nb3# ├ R1g2+ ─────── N1e2# ┌ Kc2! threat Found ┼ Bf5+ Match ── Ne4# │ ├ bxc3 Match ── Bxc3# │ └ R5g2+ ─────── N3e2# Start ┤ │ ┌ Kb1 Match ─── Nd2# ├ Ne4+? Found ──────┤ │ └ Rxe5! Match │ ┌ N1e2# └ -- ──────────────── R1g2 ───────┼ Nd3# └ N1a2#- We need to eliminate the lines that match in virtual play, and we can achieve that by looking back in the line for a position marked by the NAG that indicates the key. The find filter will do that for us (there must be a dozen other methods, all of them equally unappealing), and with the added bonus that it will allow matches in cooked lines.
cql(quiet variations) position 0:wtm result 1-0 player black "#2" {move to [f5,c3,b1,e5] comment("Match")} == 2 and comment("Found") find <-- hascomment "$1"- The end result is not exactly elegant, but it does work. One of the more obvious downsides to this approach is that the preamble is evaluated for every node in the tree. When the outer traversal is anchored at the starting position, it is evaluated just once.
┌ -- ───────── Nb3# ├ R1g2+ ────── N1e2# ┌ Kc2! threat Found ┼ Bf5+ Match ─ Ne4# │ ├ bxc3 Match ─ Bxc3# │ └ R5g2+ ────── N3e2# Start ┤ │ ┌ Kb1 ──────── Nd2# ├ Ne4+? ────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ──────────────── R1g2 ──────┼ Nd3# └ N1a2#-
The question is, why would one want to go down this road? We don't know, offhand, but crafting queries in CQL-land can often take a surprising turn. As an exercise, though, the challenge of matching complex lines of play sans line filters can be very educational. (And just a little bit masochistic.)
As indicated above, in a variations context we need to be aware of the linearization rule associated with this filter. The online reference addresses the issue at some length, and we dedicate a section below to its application.
- The echo filter
- The echo filter visits every other position in the game tree regardless of the current position. The inner traversal is in outer traversal order, and may include the current position. This filter can be rather inefficient with compute cycles unless one narrows the scope of the full evaluation of the body of the filter with some qualifying condition.
cql(quiet variations) initial echo(source target) {comment("echo " positionid)}┌ -- echo 2 ───── Nb3# echo 3 ├ R1g2+ echo 4 ── N1e2# echo 5 ┌ Kc2! threat echo 1 ┼ Bf5+ echo 6 ─── Ne4# echo 7 │ ├ bxc3 echo 8 ─── Bxc3# echo 9 │ └ R5g2+ echo 10 ─ N3e2# echo 11 Start ┤ │ ┌ Kb1 echo 13 ─── Nd2# echo 14 ├ Ne4+? echo 12 ─────┤ │ └ Rxe5! echo 15 │ ┌ N1e2# echo 18 └ -- echo 16 ───────── R1g2 echo 17 ─┼ Nd3# echo 19 └ N1a2# echo 20- The following query anchors at a key with a threat (the source position), then narrows the target range for evaluation of the body of the filter to descendants of the anchor (i.e., actual play).
cql(quiet variations) move previous primary and hascomment "threat" comment("source " positionid) echo(source target) {ancestor(source target) comment("target " positionid)}- Note that the inner traversal still covers the entire tree, but that the ancestor filter quickly dismisses the non-descendant nodes. Other qualifying criteria may just as easily be employed, perhaps targeting a different solution phase in search of an interphase theme.
┌ -- target 2 ───── Nb3# target 3 ├ R1g2+ target 4 ── N1e2# target 5 ┌ Kc2! threat source 1 ┼ Bf5+ target 6 ─── Ne4# target 7 │ ├ bxc3 target 8 ─── Bxc3# target 9 │ └ R5g2+ target 10 ─ N3e2# target 11 Start ┤ │ ┌ Kb1 ───────────── Nd2# ├ Ne4+? ───────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ─────────────────── R1g2 ───────────┼ Nd3# └ N1a2#- We should emphasize, here, that the echo filter is typically not the inner filter of choice for most queries in the problem domain.
Practical application
We'll show a few simple examples of the practical use of the techniques demonstrated in the previous sections. The same techniques are also abundantly in use throughout the latter half of the main document.
- The position-centric paradigm
- Suppose we simply wish to count the number of variations in actual play following a key with a threat. Easy enough, one might think. Count the number of distinct moves — from the key position — that follow along a secondary line of play. Let's try that.
cql(quiet variations alwayscomment) initial wtm result 1-0 line --> move primary // the key --> hascomment "threat" and find all {move secondary and comment("(Match)")}- First, we anchor the outer traversal to the starting position of a direct mate. Then, for the inner traversal, we restrict the moves to secondaries because we know that the primary move following a threat is a null move.
┌ -- ──── Nb3# ├ R1g2+ ─ N1e2# ┌ Kc2! threat (Match) ┼ Bf5+ ── Ne4# │ ├ bxc3 ── Bxc3# │ └ R5g2+ ─ N3e2# Start ┤ │ ┌ Kb1 ─── Nd2# ├ Ne4+? ──────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ────────────────── R1g2 ─┼ Nd3# └ N1a2#-
Not quite what we were expecting. The query looks to be perfectly reasonable and, indeed, the source of the problem turns out to be a matter of habit — that of viewing the game as a collection of moves.
The query matches a single position regardless of the number of variations in actual play. In fact, the find all filter returns a value of only 1 because all post-key secondary moves are made from that one position.
Remembering that CQL matches positions, we'll modify the query ever so slightly to get the result we're looking for.
cql(quiet variations alwayscomment) initial wtm result 1-0 line --> move primary // the key --> hascomment "threat" and find all {move secondary previous and comment("(Match)")}- Now the find all filter matches and counts positions for which there is a secondary move leading to the position. The distinction is subtle (and even mind bending at first), but a grasp of the concept is essential. We are not matching moves, but positions.
┌ -- ──────────── Nb3# ├ R1g2+ (Match) ─ N1e2# ┌ Kc2! threat ┼ Bf5+ (Match) ── Ne4# │ ├ bxc3 (Match) ── Bxc3# │ └ R5g2+ (Match) ─ N3e2# Start ┤ │ ┌ Kb1 ─────────── Nd2# ├ Ne4+? ──────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ────────── R1g2 ─────────┼ Nd3# └ N1a2#- Note that we've simplified the query for clarity's sake. As given, it also matches secondaries at greater depth if they are present. One can correct that deficiency in any number of ways. To give just a few possibilities: 1) ensure that the matching positions are at ply 2, or are the immediate children of or are at a distance of 1 from the key position, or 2) eliminate the find filter and add a third constituent to the line filter, accumulating the count in a variable. The find all filter is not strictly necessary. We use it because it does the counting for us.
- The implicit theme
-
There may exist patterns or characteristics of a solution tree that are suggestive of a problem expressing some particular [class of] thematic play. The pattern may or may not have any direct correlation with a particular theme, but searching on any significant pattern is likely to yield a collection of problems expressing similar themes.
As an example, the query below yields a collection of direct-mates-in-two in which both set play and actual play have some number of dual-free lines of play falling within a range, for those problems in which the key is a block.
cql(quiet variations) initial wtm result 1-0 player black "#2" Min = 4 Max = 4 function Countem() { // Line's of play are dual-free. not find {terminal and move secondary previous} // Lines of play fall within a range. Min <= {find all {terminal}} <= Max } line // actual play --> move primary --> hascomment "block" and Countem() line // set play --> move null --> Countem()-
We employ a system of nested inner traversals (the find filters nested within the scope of the line filters) anchored at the starting position. The query actually will filter on a range (established by the variables Min and Max), but we're especially interested in solutions having the same fixed number of variations in either phase.
The query stipulates nothing specific about thematic play, and yet, on little more than casual inspection of one of the matching problems, we can pick up on a rather common theme in the direct-mate genre (Amirov, Talip (To Mat - 1962)). The filtered problems are prime candidates for interphase traversals, matching themes with some very specific properties.
┌ c3 ──── Qb4# ├ e3 ──── Qf4# ┌ Qxd6! block ┤ │ ├ b5 ──── Qc5# │ └ f5 ──── Qe5# │ ┌ c3 ──── Qa4# │ ├ e3 ──── Qg4# ├ h6? block ──┼ b5 ──── Qxa7# │ ├ f5 ──── Qxg7# │ └ gxh6! │ ┌ -- ──── Qd1# ├ Qa4? threat ┤ │ └ e3! │ ┌ Qxc3# Start ┤ ┌ c3 ───┤ │ │ └ bxc3# ├ Qc7? block ─┼ b5 ──── Qxa7# │ ├ f5 ──── Qxg7# │ └ e3! │ ┌ e3 ──── Qxe3# │ ├ b5 ──── Qxa7# ├ Qe7? block ─┤ │ ├ f5 ──── Qxg7# │ └ c3! │ ┌ c3 ──── Qa4# │ ├ e3 ──── Qg4# └ -- ─────────┤ ├ b5 ──── Qxa7# └ f5 ──── Qxg7#
- Interphase traversal
-
Thematic play will often extend across phases. For example, set play may be thematically intertwined with actual play when respective lines mutate in some way, giving rise to changed play.
We give a generic language construct for interphase traversal of direct-mate solutions, allowing for the detection of thematic play across phases. The construct employs nested line filters to achieve the effect, where the level of nesting may extend well beyond that indicated (see the Lacny example from the online reference).
cql(quiet variations alwayscomment) initial wtm result 1-0 // Recover set play. line --> move null --> Set = currentposition // Actual play with nested set play traversal. line --> move primary // the key --> . --> {C = currentposition comment("Actual Play") Set:{line --> . --> {comment("Set Play") message(C)}}}-
Anchoring the outer traversal at the starting position, we first recover the node at the root of set play and capture the id of that position with a variable. Then, for each child of the key position we visit every child of that root node.
The CQL engine has tagged every matching position with a comment indicating the respective position id. This is a side effect of the message filter.
┌ c3 Actual Play ────── Qb4# ├ e3 Actual Play id:4 ─ Qf4# ┌ Qxd6! block ┤ │ ├ b5 Actual Play id:6 ─ Qc5# │ └ f5 Actual Play id:8 ─ Qe5# │ ┌ c3 ────────────────── Qa4# │ ├ e3 ────────────────── Qg4# ├ h6? block ──┼ b5 ────────────────── Qxa7# │ ├ f5 ────────────────── Qxg7# │ └ gxh6! │ ┌ -- ────────────────── Qd1# ├ Qa4? threat ┤ │ └ e3! │ ┌ Qxc3# Start ┤ ┌ c3 ─────────────────┤ │ │ └ bxc3# ├ Qc7? block ─┼ b5 ────────────────── Qxa7# │ ├ f5 ────────────────── Qxg7# │ └ e3! │ ┌ e3 ────────────────── Qxe3# │ ├ b5 ────────────────── Qxa7# ├ Qe7? block ─┤ │ ├ f5 ────────────────── Qxg7# │ └ c3! │ ┌ c3 Set Play id:42 ─── Qa4# │ ├ e3 Set Play id:44 ─── Qg4# └ -- ─────────┤ ├ b5 Set Play id:46 ─── Qxa7# └ f5 Set Play id:48 ─── Qxg7#- The output from the message filter includes the position id correlating with the id given in the PGN result rendered in tree format above. On examination of the output, one notices that the CQL engine repeatedly visits each line in set play for every line in actual play, thus iterating over the tree in a fashion as if in a nested loop.
Game: 1 move 2(wtm)[42]: move 2(wtm) Game: 1 move 2(wtm)[44]: move 2(wtm) Game: 1 move 2(wtm)[46]: move 2(wtm) Game: 1 move 2(wtm)[48]: move 2(wtm) Game: 1 move 2(wtm)[42]: move 2(wtm)[4] Game: 1 move 2(wtm)[44]: move 2(wtm)[4] Game: 1 move 2(wtm)[46]: move 2(wtm)[4] Game: 1 move 2(wtm)[48]: move 2(wtm)[4] Game: 1 move 2(wtm)[42]: move 2(wtm)[6] Game: 1 move 2(wtm)[44]: move 2(wtm)[6] Game: 1 move 2(wtm)[46]: move 2(wtm)[6] Game: 1 move 2(wtm)[48]: move 2(wtm)[6] Game: 1 move 2(wtm)[42]: move 2(wtm)[8] Game: 1 move 2(wtm)[44]: move 2(wtm)[8] Game: 1 move 2(wtm)[46]: move 2(wtm)[8] Game: 1 move 2(wtm)[48]: move 2(wtm)[8]
- The block-threat
- A block-threat is a composition in which a complete block cannot be solved by a waiting move but requires a key with a threat. As a complete block, all legal moves for black in the starting position must be set with mate. The following query matches such a problem for a direct-mate-in-two.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" // Count the number of legal moves in the current position (btm). function Countem() { Count = 0 piece Piece in a { Count += #(move to . from Piece legal) // Adjust the count to include all possible promotions. Count += #(move to [a-h1] from (Piece&p) legal) * 3 } Count } // The key is not a waiting move. line --> move primary // the key --> hascomment "threat" // All legal moves are set. SetMoves = 0 line --> move null --> LegalMoves = Countem() --> SetMoves += 1 LegalMoves == SetMoves-
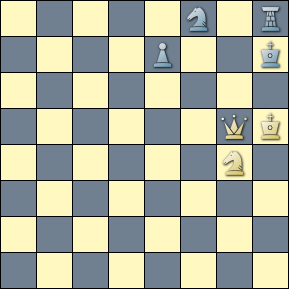With the outer traversal anchored at the starting position, we first ensure that the key is a threat and we then recover set play to determine that every legal move is set. In counting the number of lines set with mate, we take advantage of the line filter's inner traversal to count them one by one (the third constituent).
The solution for the composition depicted in the diagram (Sándor Boros (Magyar Sakkvilág - 1926)) matches the query, with the rendered solution tree showing all legal black moves set with mate.
┌ -- ───── Qxe7# ├ Ne6 ──── Qg6# ┌ Nh6! threat ┤ │ ├ Ng6 ──── Qxg6# │ └ Rg8 ──── Qxg8# ├ Nf6+? ─────── exf6! │ ┌ Nd7 ──── Qg6# │ ├ Ne6 ──── Qg6# ├ Ne5? block ─┼ Ng6 ──── Qxg6# │ ├ Rg8 ──── Qh6# │ └ e6! Start ┤ ├ Qh6+? ─────── Kg8! ├ Qxe7+? ────── Kg8+! ├ Qg7+? ─────── Kxg7+! ├ Qg6+? ─────── Nxg6! │ ┌ e5 ───── Nf6# │ ├ e6 ───── Nf6# │ ├ Nd7 ──── Qg6# └ -- ─────────┤ ├ Ne6 ──── Qg6# ├ Ng6 ──── Qxg6# └ Rg8 ──── Qh6#
- Example template
- Explanation...
syntax
result
- Example template
- Explanation...
syntax
result
- Intraphase traversal
- We've already seen how nested line filters may be employed for interphase traversals. Here, we'll nest an echo filter within a line filter for a similar effect, but within a single phase as we wish to "capture" both traversals as they walk the same set of terminal positions. We'll capture the line filter's traversal as it evaluates it's terminal constituent, and we'll capture the echo filter's traversal as its targets satisfy some set of predetermined conditions.
// Intraphase traversal. cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> move primary // the key --> Actual = currentposition // root of actual play --> not move null previous // no threat lines --> echo(source target) { terminal and ancestor(Actual target) parent:{not move null previous} message("source:" source) }-
As the echo filter walks the solution tree, we quickly dismiss any target positions that are not in actual play or are not a terminal position. We also carefully filter out any consideration of threat lines in our determination of relevant source/target pairs.
Note that if we were employing nested line filters, the anchor of the inner line would have to be at or before the terminal positions' common LCA. With the echo filter traversing the entire tree, we need only to ensure that the LCA (with the Actual variable as a reference) is an ancestor of each of our targets of interest.
┌ -- ──── Nb3# ├ R1g2+ ─ N1e2# id:5 ┌ Kc2! threat ┼ Bf5+ ── Ne4# id:7 │ ├ bxc3 ── Bxc3# id:9 │ └ R5g2+ ─ N3e2# id:11 Start ┤ │ ┌ Kb1 ─── Nd2# ├ Ne4+? ──────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ────────── R1g2 ─┼ Nd3# └ N1a2#- Note that the echo filter's source variable tracks the line filter's traversal as it evaluates each terminal node's respective constituent. The message filter then automatically tags every message with what is, effectively, the position bound to the echo filter's target variable.
Game: 1 move 2(btm)[7]: source:move 2(btm)[5] Game: 1 move 2(btm)[9]: source:move 2(btm)[5] Game: 1 move 2(btm)[11]: source:move 2(btm)[5] Game: 1 move 2(btm)[5]: source:move 2(btm)[7] Game: 1 move 2(btm)[9]: source:move 2(btm)[7] Game: 1 move 2(btm)[11]: source:move 2(btm)[7] Game: 1 move 2(btm)[5]: source:move 2(btm)[9] Game: 1 move 2(btm)[7]: source:move 2(btm)[9] Game: 1 move 2(btm)[11]: source:move 2(btm)[9] Game: 1 move 2(btm)[5]: source:move 2(btm)[11] Game: 1 move 2(btm)[7]: source:move 2(btm)[11] Game: 1 move 2(btm)[9]: source:move 2(btm)[11]
-
So why are we going through all of this pain? As it happens, it's not at all unusual for a theme to call for all mating lines or mating moves to be unique within the scope of a particular phase. Nested iterations over the terminal positions is just what the solver ordered, and is what we might subconsciously be doing if we were inspecting the solution tree without the aid of CQL.
The next query expands on the basic query above to search for problems having all mates in actual play coming from a queen and coming on a unique square. We'll set a lower bound on the number of mating lines and sort the matching problems by that number.
// Intraphase traversal. cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" Q == 1 // only one queen on the board Terms = 0 Uniqs = 0 line --> move primary // the key --> { // actual play Actual = currentposition // All mates are by the queen. not find {terminal move from ~Q previous} } --> not move null previous // threat lines are irrelevant --> { // the terminal position Terms += 1 // Eliminate discoveries. k attackedby Q // Is the mating square unique? not echo(source target) { terminal and ancestor(Actual target) parent:{not move null previous} source < target source:Q & target:Q } Uniqs += 1 comment("Unique") } // All mating squares are unique with a lower bound. 6 <= Terms == Uniqs sort "Unique mating squares" Uniqs-
Note that it is not enough only to ensure that the terminal move is by a queen. We must additionally stipulate that it is the queen that is mating. That is, the queen move did not simply uncover a mate by discovery.
Also observe that we've added a condition to the qualification of the echo filter's target position, namely source < target. Without that condition, we would be repeating evaluations of the balance of the body of the filter for some number of source/target pairs. (See the message dump above for verification.)
The query matches a composition by Benko (Magyar Sakkélet - 1984), where pawn play is also a part of the theme. Eight lines. Clean. Efficient. Disgusting.
┌ a2 ──── Qb2# Unique ├ b3 ──── Qc3# Unique ├ e3 ──── Qxe3# Unique ├ c4 ──── Qd4# Unique ┌ Nb5! block ─┤ │ ├ g4 ──── Qf4# Unique │ ├ cxb5 ── Qd5# Unique │ ├ h5 ──── Qxg5# Unique Start ┤ └ e6 ──── Qd6# Unique │ ┌ -- ──── Qxc5# ├ Qe3? threat ┤ │ └ Kd6! ├ Qd5+? ─────── cxd5! │ ┌ Ng4# │ ┌ -- ───┤ │ │ └ Nc4# └ Ne3? threat ┤ ├ h5 ──── Nc4# └ Kf4!-
Why the echo filter? The criteria fairly scream out for the line or the find filters (Actual:line... or Actual:find...).
While we make no excuses for the echo's inefficiencies, there are a couple of intangibles which we shall offer up without explanation. The filter is clean. The filter is clear. And the filter manages our position variables for us, while automatically eliminating the current position from the traversal. And we are, by our nature, lazy critters with an affinity for clean things. In short, it boils down to a matter of taste.
We should finish with the footnote that an essential element in employing the echo is the quick dismissal of unwanted targets. In that regard, the ordering of the leading filters matters. Filters with the least overhead and with the greatest impact should go up front.
We might also annoyingly point out the obvious... that if the theme manifests strictly in actual play, then solutions with very little virtual play suffer a less severe penalty. Solutions with no virtual play are even better. Toward that end — if one finds that one is irresistibly drawn to the echo filter — one might consider solving the database to include just one phase in the solution (actual play).
All of that said, this query would look very different and would likely (maybe) be much more efficient if the find all filter could (optionally) return a set of positions. Then nested iterating position filters (much like the square filter) might be employed, at least in our fantasies, to achieve our ends without all of this repetitious traversing of the tree. While acknowledging that CQL was never designed or intended for the problem domain with its zillions of variations, it is a remarkably adaptable language. We're just thinking out loud (influenced, no doubt, by that tiresome kibbitzing niece), thinking ahead, to that version 7 release when our CQL developers are retired and have nothing better to do than to go trout fishing on some pristine lake in the Himalayas. Bring along your laptops, gentlemen.
- Post mortem: No matter how brilliant [sic] the idea, there will always be a better idea. While we're willing to admit that our brain is growing weak with age, the following technique — which we shall borrow from an online example — is not exactly intuitively obvious to the mere mortal (thanks go out to Lewis Stiller for the idea).
// Intraphase traversal. cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" function Unique(Square Set) { not Square in Set Set = Square | Set // insert Square into Set } Terms = 0 Uniqs = ~. // the empty set (not Uniqs = []) line --> move primary // the key --> { // actual play Actual = currentposition Q == 1 // only one queen on the board // All mates are by the queen. not find {terminal move from ~Q previous} } --> not move null previous // threat lines are irrelevant --> { // the terminal position Terms += 1 // Eliminate discoveries. k attackedby Q // Is the mating square unique? Unique(Q Uniqs) comment("Unique") } // All mating squares are unique with a lower bound. 6 <= Terms == Uniqs sort "Unique mating squares" Uniqs- The function accomplishes two things in particular: 1) it maintains a record of the set of mating squares, and 2) it ensures that the square given in the parameter list is unique vis-à-vis that set. Putting the function to work as the line filter visits each terminal position, we can avoid the echo traversal entirely.
- A threat storm
- Expanding on the notion of an implicit theme, let's consider searching on some more-or-less arbitrary set of chacracteristics in the solution tree and see what flavor of thematic play pops up. The next query matches a direct-mate-in-two in which every try with a threat in virtual play matches the key threat.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" // Compare two moves. function SameMove(X Y) { X:{move from . previous} == Y:{move from . previous} X:{move to . previous} == Y:{move to . previous} // Account for promotions. X:{type move to . previous} == Y:{type move to . previous} } // Eliminate trees with duals in threats. not find {move null primary previous and move secondary} // Recover the key threat. line primary --> . // the key --> hascomment "threat" --> move null previous --> mate and Threat = currentposition matchCount = 0 threatCount = 0 // Match threats in virtual play with the key threat. line --> move secondary --> hascomment "$2" and hascomment "threat" --> move null previous and threatCount += 1 --> {mate SameMove(currentposition Threat) matchCount += 1 comment("Match")} // Every threat matches and the counts are in range. 4 <= matchCount == threatCount <= 8-
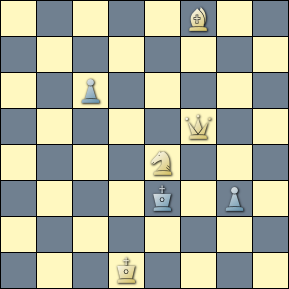Being novices, we have no particular reason to believe that this set of criteria should be suggestive of thematic play. But on inspection of the filtered problems, we can see that the query just happens to match a composition by Adolphi (Austrums - 1897) in which a wheeling white knight tries and tries and tries to deny the flight square — always with the same threat and always with the same refutation — but for the flight-taking key. The query says absolutely nothing about flights or wheeling knights, only that the same threat propagates across all phases.
┌ -- ─── Bc5# ┌ Nf2! threat ─┤ │ └ Kd4 ── Qc5# │ ┌ -- ─── Bc5# Match ├ Nc3? threat ─┤ │ └ Kd4! │ ┌ -- ─── Bc5# Match ├ Nd2? threat ─┤ │ └ Kd4! Start ┤ ┌ -- ─── Bc5# Match ├ Nxg3? threat ┤ │ └ Kd4! │ ┌ -- ─── Bc5# Match ├ Ng5? threat ─┤ │ └ Kd4! │ ┌ -- ─── Bc5# Match ├ Nf6? threat ─┤ │ └ Kd4! └ Bc5+? ──────── Kd3!-
As given, what we have is but a rudimentary interphase pattern-matcher demonstrating a traversal technique (which is the point of this document). But we've also demonstrated (though trivially) that thematic play may leave lying about incidental patterns in the solution tree that may be useful in filtering out a collection of problems having a common set of interesting features.
Of course, a pursuit of this line of inquiry can be a decadent passtime that might well shamefully occupy an entire lifetime. We like to put the blame on CQL for enabling it in the first place. ("Sweetheart, could you take out the trash?")
Linearization
Linearization is a complex topic, and in most situations one need be only vaguely aware of it. Nonetheless, to fully appreciate the traversal patterns that one might witness with the line filter, it can be useful to have at least a superficial understanding of the rule.
The online reference includes a section on linearization that will help to explain the rationale for the rule. We'll expand on that material to demonstrate the rule's impact on a full solution tree. Then we'll explore some of the reasons that one might wish to disable linearization and give a couple of relevant examples.
- With linearization enabled, we can give a specific sequence of moves to match and reliably expect that there will be no surprises in the result.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> {message("pid:" positionid) move to c2 comment("Match")} --> {message("pid:" positionid) move to g2 comment("Match")} --> {message("pid:" positionid) move to e2 comment("Match")} --> {message("pid:" positionid) mate}- The solution tree has two distinct lines of play that match every constituent of the line filter.
┌ -- ──────────────── Nb3# ├ R1g2+ Match id:4 ── N1e2# Match id:5 ┌ Kc2! threat Match ┼ Bf5+ ────────────── Ne4# │ ├ bxc3 ────────────── Bxc3# │ └ R5g2+ Match id:10 ─ N3e2# Match id:11 Start ┤ │ ┌ Kb1 ─────────────── Nd2# ├ Ne4+? ────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ──────────────── R1g2 ─────────────┼ Nd3# └ N1a2#- The output from the message filters clearly shows the breakdown of the lines of play resulting from linearization. Study the sequence of evaluations carefully. From position 0 (the starting position) we have three possible moves, and from position 1 (the key) we have five. One can see that the CQL engine is traversing the tree line by line as each of the constituents of the line filter matches its respective positions.
Game: 1 move 1(wtm): pid:0 Game: 1 move 1(btm): pid:1 Game: 1 move 1(btm): pid:1 Game: 1 move 2(wtm)[4]: pid:4 Game: 1 move 2(btm)[5]: pid:5 Game: 1 move 1(btm): pid:1 Game: 1 move 1(btm): pid:1 Game: 1 move 1(btm): pid:1 Game: 1 move 2(wtm)[10]: pid:10 Game: 1 move 2(btm)[11]: pid:11 Game: 1 move 1(wtm): pid:0 Game: 1 move 1(wtm): pid:0
- For contrast, let's disable linearization across the entire body of the query by giving the nolinearize pseudo-parameter in the CQL header.
cql(quiet variations alwayscomment nolinearize) initial wtm result 1-0 player black "#2" line --> {message("pid:" positionid) move to c2 comment("Match")} --> {message("pid:" positionid) move to g2 comment("Match")} --> {message("pid:" positionid) move to e2 comment("Match")} --> {message("pid:" positionid) mate}- We find that we're now also matching a line in set play far removed from the key. Without linearization, the move filter from the first constituent of the line filter evaluates as true for positions matching all trailing constituents.
┌ -- ──────────────── Nb3# ├ R1g2+ Match id:4 ── N1e2# Match id:5 ┌ Kc2! threat Match ┼ Bf5+ id:6 ───────── Ne4# │ ├ bxc3 id:8 ───────── Bxc3# │ └ R5g2+ Match id:10 ─ N3e2# Match id:11 Start ┤ │ ┌ Kb1 ─────────────── Nd2# ├ Ne4+? id:12 ──────┤ │ └ Rxe5! │ ┌ N1e2# Match id:18 └ -- id:16 ────────── R1g2 Match id:17 ─┼ Nd3# id:19 └ N1a2# id:20- Notice the change in the line filter's traversal of the tree. Missing are the repeated evaluations at positions 0 and 1. Position 0 is evaluated just once, as is position 1. Because both of the respective constituents for those positions evaluate to true, matches may occur across branches of the tree regardless of node ancestry.
Game: 1 move 1(wtm): pid:0 Game: 1 move 1(btm): pid:1 Game: 1 move 2(wtm): pid:2 Game: 1 move 2(wtm)[4]: pid:4 Game: 1 move 2(btm)[5]: pid:5 Game: 1 move 2(wtm)[6]: pid:6 Game: 1 move 2(wtm)[8]: pid:8 Game: 1 move 2(wtm)[10]: pid:10 Game: 1 move 2(btm)[11]: pid:11 Game: 1 move 1(btm)[12]: pid:12 Game: 1 move 1(btm)[16]: pid:16 Game: 1 move 2(wtm)[17]: pid:17 Game: 1 move 2(btm)[18]: pid:18 Game: 1 move 2(btm)[19]: pid:19 Game: 1 move 2(btm)[20]: pid:20
- If, instead of disabling linearization, we change the sequence of moves as given below, the query fails to match any of the lines of play (as we would hope and expect).
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> {message("pid:" positionid) move to c2 comment("Match")} --> {message("pid:" positionid) move to g2 comment("Match")} --> {message("pid:" positionid) move to c3 comment("Match")} --> {message("pid:" positionid) mate}- Let's look at what happens with linearization disabled on just the second constituent.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> {message("pid:" positionid) move to c2 comment("Match")} --> currentposition:{message("pid:" positionid) move to g2 comment("Match")} --> {message("pid:" positionid) move to c3 comment("Match")} --> {message("pid:" positionid) mate}-
Now the move filter for the second constituent matches (twice) and that match propagates through for all evaluations that follow because the lines of play have not been isolated from one another.
Remember that the line filter continues to visit every node until some constituent in the line fails to match a position. With linearization enabled, that failure occurs at the second constituent for three of the five lines of play. Without isolation of each line, the second constituent is a match as the engine evaluates the third constituent for each of its respective positions.
┌ -- ──────────────── Nb3# ├ R1g2+ Match id:4 ── N1e2# ┌ Kc2! threat Match ┼ Bf5+ id:6 ───────── Ne4# │ ├ bxc3 id:8 ───────── Bxc3# Match id:9 │ └ R5g2+ Match id:10 ─ N3e2# Start ┤ │ ┌ Kb1 ─────────────── Nd2# ├ Ne4+? ────────────┤ │ └ Rxe5! │ ┌ N1e2# └ -- ──────────────── R1g2 ─────────────┼ Nd3# └ N1a2#- Notice that with linearization active for the first constituent of the line filter, position 0 is again visited three times, once for each of the three possible moves from that position. As such, set play and virtual play are left out of the traversal and the line in set play that would otherwise have matched the second and third constituents is never evaluated.
Game: 1 move 1(wtm): pid:0 Game: 1 move 1(btm): pid:1 Game: 1 move 2(wtm): pid:2 Game: 1 move 2(wtm)[4]: pid:4 Game: 1 move 2(wtm)[6]: pid:6 Game: 1 move 2(wtm)[8]: pid:8 Game: 1 move 2(btm)[9]: pid:9 Game: 1 move 2(wtm)[10]: pid:10 Game: 1 move 1(wtm): pid:0 Game: 1 move 1(wtm): pid:0
- Just to reinforce the point, let's take matters to an extreme and disable linearization for the line filter's first constituent, as well. We'll also modify the move sequence to an utterly absurd line, crossing phases and even branches within the phase.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" line --> currentposition:{message("pid:" positionid) move to c2 comment("Match")} --> currentposition:{message("pid:" positionid) move to e5 comment("Match")} --> {message("pid:" positionid) move to d2 comment("Match")} --> {message("pid:" positionid) mate}- With linearization disabled all around (this time by constituent rather than with the nolinearize parameter), we first match the key, then the refutation of the try, and finally the terminal node of the branch opposite the refutation. None of the matching positions is in the same line of play.
┌ -- ──────────────── Nb3# ├ R1g2+ ───────────── N1e2# ┌ Kc2! threat Match ┼ Bf5+ ────────────── Ne4# │ ├ bxc3 ────────────── Bxc3# │ └ R5g2+ ───────────── N3e2# Start ┤ │ ┌ Kb1 id:13 ───────── Nd2# Match id:14 ├ Ne4+? id:12 ──────┤ │ └ Rxe5! Match id:15 │ ┌ N1e2# └ -- id:16 ────────── R1g2 ─────────────┼ Nd3# └ N1a2#- It's worth noting that the engine visits position 14 and registers that match before even visiting position 15. The positions are evaluated for their respective constituents in regular traversal order, with or without linearization. The difference is that — with linearization enabled — any given position may be visited multiple times, once for each distinct line of isolated play that includes the position.
Game: 1 move 1(wtm): pid:0 Game: 1 move 1(btm): pid:1 Game: 1 move 1(btm)[12]: pid:12 Game: 1 move 2(wtm)[13]: pid:13 Game: 1 move 2(btm)[14]: pid:14 Game: 1 move 2(wtm)[15]: pid:15 Game: 1 move 1(btm)[16]: pid:16
So why would one ever want to disable linearization? There will be times when we wish to know that some specific set of moves emanate from a single position and — though we could almost certainly achieve our ends with linearization in place — it might be simpler without.
- Wheeling knights
- We distinguish, here, between knight wheels as a theme and a general maneuver by a knight where some number of the spokes of the knight's wheel show up in the solution. The query below matches a problem with a black knight completing a full wheel in both actual and set play. Any thematic considerations are left out of the query.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#2" n == 1 line --> move primary --> find {move to (orthogonal 1 orthogonal 2 n) from n} == 8 line --> move null --> find {move to (orthogonal 1 orthogonal 2 n) from n} == 8-
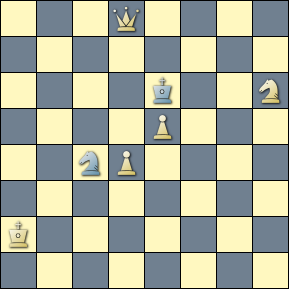We keep things simple by first ensuring that there is only one black knight on the board. We would otherwise have to employ a piece filter to iterate over the knights one by one.
The move filters return the number of knight moves (actually, the set of squares to which the moves are made) that are tallied across lines of play, with linearization disabled for their respective filters due to their presence in the body of a find filter. The nested orthogonal filters yield a set that is slightly outside the range of the knight's legal moves, but with no harm done. (By the way, one could as easily generate the precise set by substituting (move to . from n legal) for the nested orthogonals, but that would be less interesting.)
The query matches a complete block by Antipov (Sa ogneupory - 1987) where the wheeling knight leaves actual play unchanged from the set mates.
┌ Na3 ─── Qd6# ├ Nb2 ─── Qd6# ├ Nd2 ─── Qd6# ├ Ne3 ─── Qd6# ┌ Ka1! block ┤ │ ├ Nxe5 ── d5# │ ├ Nd6 ─── Qxd6# │ ├ Nb6 ─── Qd6# │ └ Na5 ─── Qd6# ├ d5+? ─────── Kxe5! ├ Qd6+? ────── Nxd6! Start ┤ ├ Qd7+? ────── Kxd7! ├ Qe8+? ────── Kd5! │ ┌ Na3 ─── Qd6# │ ├ Nb2 ─── Qd6# │ ├ Nd2 ─── Qd6# │ ├ Ne3 ─── Qd6# └ -- ────────┤ ├ Nxe5 ── d5# ├ Nd6 ─── Qxd6# ├ Nb6 ─── Qd6# └ Na5 ─── Qd6#- N.B. A certain formerly favorite niece of ours, that niece who is too busy to lend a hand with her brilliant writing skills, that niece who flatly denies that she knows anything about CQL, that niece who loves to kibbitz during (but not limited to) blitz games, yes, that niece, has ever so gently pointed out to us that we are making things far more complicated than they need to be. That, in fact, find {move to . from n} == 8 is sufficient to get the job done. Not to be outdone, we answered with instant retort that, of course, we knew that, but that simple is so boring. We're not sure that she bought it.
- Promotion play
- One of the more obvious sets of moves that we might wish to match is the set of all possible promotions emanating from some one position, across some collection of variations in the solution tree. The query below matches a direct-mate-in-3 in which black's promotion play is countered (in some line) by white's promotion play, both sides promoting to all four possibilities in actual play.
cql(quiet variations alwayscomment) initial wtm result 1-0 player black "#3" line --> move primary // the key --> currentposition:{ move promote Q move promote R move promote B move promote N } --> currentposition:{ move promote Q move promote R move promote B move promote N }-
Linearization is disabled for both promotion constituents so that we can match positions from which all four promotions are realized.
Problems exhibiting such counter promotion play are rare, so we should not be surprised that one of the matching compositions belongs to that master of promotion play, Peter Hoffmann (Die Schwalbe - 2014).
The solution tree for this composition is quite large, so we present just a slice of it showing white's response to black's promotion to rook. The full solution may be found in the meson problem database on the SourceForge project site.
│ ┌ Qd5# │ ├ Qxh7# │ ┌ -- ──┤ │ │ ├ Qxg5# │ │ └ Ne7# │ │ ┌ Qxh7# │ ├ Rd1 ─┼ Qxg5# │ │ └ Ne7# │ ├ Bb5+ ─ Qxb5# │ │ ┌ Qxh7# │ ├ Bc4 ─┼ Qxg5# │ │ └ Ne7# │ │ ┌ Qd5# │ ├ Rxc7 ┼ Qxg5# │ │ └ Be4# │ ┌ fxg8=Q threat ┤ ┌ Qd5# │ │ │ ├ Qh7# │ │ ├ h6 ──┤ │ │ │ ├ Qg6# │ │ │ └ Ne7# │ │ │ ┌ Qe6# │ │ │ ├ Qf7# │ │ ├ Nc6 ─┤ │ │ │ ├ Qxh7# │ │ │ └ Qxg5# │ │ │ ┌ Qxe6# │ │ │ ├ Qf7# │ │ ├ Ne6 ─┤ │ │ │ ├ Qxh7# │ │ │ └ Ne7# ├ e1=R ─┤ │ ┌ Qxf7# │ │ └ Nf7 ─┼ Qxh7# │ │ └ Ne7# │ │ ┌ Nge7# │ │ ┌ -- ──┼ Nh6# │ │ │ └ Nce7# │ │ ├ Bb5+ ─ Qxb5# │ ├ fxg8=N threat ┤ ┌ Nh6# │ │ ├ Rxc7 ┤ │ │ │ └ Be4# ┌ Rg4! threat ───┤ │ ├ Nc6 ── Nh6# │ │ │ │ ┌ Nge7# │ │ │ └ Nf7 ─┤ │ │ │ └ Nce7# │ │ │ ┌ R8xg5# │ │ │ ┌ -- ──┤ │ │ │ │ └ Ne7# │ │ │ ├ Bb5+ ─ Qxb5# │ │ │ │ ┌ R8xg5# │ │ │ ├ Rxc7 ┤ │ │ ├ fxg8=R threat ┤ └ Be4# │ │ │ ├ h6 ─── Ne7# │ │ │ ├ Nc6 ── R8xg5# │ │ │ ├ Ne6 ── Ne7# │ │ │ └ Nf7 ── Ne7# │ │ │ ┌ Bxh7# │ │ │ ┌ -- ──┤ │ │ │ │ └ Ne7# │ │ │ ├ Bb5+ ─ Qxb5# │ │ └ fxg8=B threat ┤ │ │ ├ Rxc7 ─ Be4# │ │ │ ┌ Be6# │ │ └ Nc6 ─┤ │ │ └ Bxh7#
See also
Credits
This document is Copyright (c) 2019-2024 Lionel Hampton. The Chess Query Language was originally developed by Gady Costeff and Lewis Stiller. The upstream Scid vs PC project is managed by Steven Atkinson.
The diagrams appearing in this document were created with the Scid vs PC application's board screenshot facility. The piece set is included with that application and is credited on the project's site.