Handling Twins in a CQL Universe

This document (still under development) is a companion to the CQL by Example document presented on the Scid++ project site. We regret to inform that this little gem does not in any way address the many and challenging vagaries encountered in the rearing of diminutive humanoid types. Rather, we intend to demonstrate a few language techniques which may be employed in matching some simple cross-twin patterns that might manifest in a chess composition. Leaping right into that vast unknown where no CQL query has gone before, this document is not for the faint of heart.

Twinning is a device used by composers to expand the palette from which the artist paints. Normally, a theme might be expressed across phases of play (direct) or across multiple solutions (help). Within the twinning domain, a theme may also be expressed across starting positions and/or solution trees. A knight wheeling its way across phases in virtual play might instead wheel its way across twins, each spoke in the knight's wheel serving as the key to the respective twin's solution (no small feat).

Frowned upon in some circles, twinning is not just a different way of achieving the same end. It provides a means of expressing an idea that — in many cases — could not otherwise be expressed. With the release of CQL v6.1 — which we highly recommend — we can search a database of twinned compositions for many of those ideas.

The database

All of the example queries below have been executed against the twins.pgn database — which can be found with the project's support files — and will match at least a handful of problems. Every twin of every series in that database has a solution generated by the Scid++ problem solving extension (solutions by Popeye).

The structure of the metadata for each of the PGN games comprising a twin series is very specifically bound to the expectations of a cross-twin query:

The composition's base position has the string 'Twins' in the PGN Black tag and has the twin count for the series carried in the PGN BlackElo tag.
Compositions having an 'A' twin will have no solution tree in the zeroposition (i.e., will have no position with ply > 0).
The database must be sorted such that all twins in a series are in their proper order. (With the twins database provided as a project support file, the sort field is the PGN Round tag.)

For convenience, the PGN Round tag for each twin series in the support database is generated in such a way as to easily allow for the filtering of a complete series of twins based on the series' common quotient in a modulus N scheme.

Examples of cross-twin queries

We have two flavors of cross-twin pattern matching in mind: 1) patterns expressed across a series of starting positions, and 2) patterns (themes) expressed across a series of solution trees. The former is the easy stuff; the latter, not so much.

The basics

Assuming that we have a well-ordered database of twins, the following techniques may be employed to recover a series.

Series recovery
We'll be needing 1) a means for detecting the first and last member of a series, and 2) a structure within which to conduct our work. We've already pointed out above that the base position of every series is marked as having the "Twins" string in the PGN Black tag. We also get a count of the number of twins in the series carried in the PGN BlackElo tag of that base position. Thus, we provide for the first item.
The outer if-then-else filter then gives us the conditional control framework within which to initialize each series start and to process each twin in the series. The inner if-then-else filter is not strictly necessary, but gives us a flexible test structure for end-of-series processing which may require a lengthy compound filter for either clause.

The following query matches the first and last member of each series in the database, without consideration for any other criteria along the way.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
} else {
  TwinCount -= 1
  if TwinCount == 0
    then true
    else false
}

The zeroposition
If the composition gives a zeroposition as the base position, the solution for that position will be empty. The zeroposition is not intended to be solved and only serves as a starting point for each of the constituent twins. Zeroposition twinned compositions often cannot be specified by other means.
We might want to single out the zeroposition series (for whatever reason), and we can do so by checking that the PGN header includes a TwinA tag. The following query matches the first and last member of a qualifying series.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 1
  if tag "TwinA"
    then SeriesAbort = 0
    else false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Series acrobatics

A number of otherwise simple actions are complicated in a twinning context by the fact that we only know that a series is a match after processing the last twin. Several of the language facilities introduced with v6.1 allow us to handle these complications reasonably gracefully.

A common thread weaving its way through the examples below is the multipass query. Persistent data is handed off from one query to the next via a temporary file, identifying matching series and correlated information. Multiple ways of possibly structuring a multipass occur to us and we'll demonstrate a couple of those.

Note that the examples in this section require the latest incarnation of the twins database, which has had a SeqNum PGN tag added to the header. The tag carries redundant information, but is necessary because the PGN Round tag is not accessible from CQL.

Filling out the series
We've received a number of inquiries asking how one might easily fill out the series given that only the last twin of the series matches the query. The short answer is "Use the Scid++ CQL search facility." That UI will fill in each series in the game list with a single mouse click.
But for those who are executing queries from the command line, perhaps the following suggestion will be helpful. The first pass in our example writes matching sequence numbers to file for any series with six or more twins, along with a comment that is to be prepended to every twin in the series. The second pass matches all twins in a series for every sequence number passed along from the first run.

cql(quiet)

function pass1CQL() {
  initial
  if player black "Twins"
  then {
    persistent TwinCount = elo black
    persistent SeriesAbort = 0
    if TwinCount < 6 then SeriesAbort = 1
    false
  } else {
    TwinCount -= 1
    if TwinCount == 0 and SeriesAbort == 0
      then {
        writefile("/tmp/out.cqo" str(tag "SeqNum" ":"
            "Comment for sequence number " tag "SeqNum" \n))
        true
      } else false
  }
}

function pass2CQL() {
  initial
  if (gamenumber == 1) {
    dictionary Series
    SeqNums = readfile "/tmp/out.cqo"
    while (SeqNums ~~ "(.+):(.*)")  Series[\1[:6]] = \2
  }
  if Series[(tag "SeqNum")[:6]]
    then {
      comment(Series[(tag "SeqNum")[:6]])
      true
    } else false
}


pass1CQL()
//pass2CQL()

Alternately commenting and uncommenting the last two lines of the query gives us our two passes. Crude but effective.

Commenting the series
Somewhat related to the last issue is the question of how one goes about adding comments to matching positions across the series. There must be half a dozen reasonable approaches to the problem, and we'll demonstrate one of those below. The query requires two passes, the first of which we'll refer to as a dry run.
The dry run records the sequence numbers of matching series to a file, as above. The second pass matches every twin of the series marked by the dry run, with comments generated by the find filter. All of the serious work of the query is duplicated between passes, but that would seem to be unavoidable.

The example searches for series having an underpromotion in the mainline of every twin in the series. Nothing useful, just a demo.

cql(alwayscomment)
initial

if isunbound DryRun then DryRun = 1  // zero for wet run
if isunbound FD then FD = "/tmp/out.cqo"

if (DryRun == 0 and gamenumber == 1) {
  dictionary Series
  SeqNums = readfile FD
  while (SeqNums ~~ "(.+):(.*)")  Series[\1[:6]] = \2
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not find { move promote [RBN] previous } then SeriesAbort = 1
  DryRun == 0 and Series[(tag "SeqNum")[:6]]
} else {
  if not find { move promote [RBN] previous } then SeriesAbort = 1
  TwinCount -= 1
  if DryRun == 1
    then if TwinCount == 0 and SeriesAbort == 0
      then writefile(FD str(tag "SeqNum" ":"
             "Comment for sequence number " tag "SeqNum" \n))
      else false
    else Series[(tag "SeqNum")[:6]]
}

if DryRun == 0 then comment(Series[(tag "SeqNum")[:6]])

We use the DryRun variable as something of a boolean switch to distinguish between passes. That variable may be given on the command line with the -assign option. The persistent file path may also be given on the command line, or it will default to our usual.
The alwayscomment pseudo-parameter in the CQL header disables smart comments, which is only necessary because we are applying a not ahead of the find filter. If executing the query from the command line, delete the pseudo-parameter and add the alwayscomment option to the command line.

Sorting the series
And then there's the question of sorting. What does the term even mean in a twinning context? We're guessing that in most cases it means that a matching series is sorted within the overall results as a unit. Intra-series sorting doesn't make alot of sense to us, but whatever.
So, as a totally contrived scenario, suppose we have a user who is hopelessly fixated on knights in solutions. The more knight moves the better. Knights, knights, knights. So we go counting up the knight moves per twin and the knight moves per series, and of course we want to sort the results so that we get the series with the most moves up top and the twins with the most moves per series at the top of each series. Good enough.

We discard any series with fewer than 12 knight moves in the mainline. We don't care about the structure of the solution... this is just a dumb demo. In fact, we went into this little demo thinking dumb dumb dumb dumb dumb. Then we looked at the results. Some of the series at the top of the results are just very cool. Who knew?

cql()
initial

if isunbound DryRun then DryRun = 1  // zero for wet run
if isunbound FD then FD = "/tmp/out.cqo"

if (DryRun == 0 and gamenumber == 1) {
  dictionary Series
  SeqNums = readfile FD
  while (SeqNums ~~ "(.+):(.*)")  Series[\1[:6]] = \2
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  tCount = find 0 1000 { move from [Nn] previous }
  persistent sCount = tCount
  DryRun == 0 and Series[(tag "SeqNum")[:6]]
} else {
  tCount = find 0 1000 { move from [Nn] previous }
  sCount += tCount
  TwinCount -= 1
  if DryRun == 1
    then if TwinCount == 0 and sCount >= 12
      then writefile(FD str(tag "SeqNum" ":" sCount \n))
      else false
    else Series[(tag "SeqNum")[:6]]
}

if DryRun == 0 {
  sort "Knight moves (series)" int(Series[(tag "SeqNum")[:6]])
  sort min "Series" (tag "SeqNum")[:6]
  sort "Knight moves (twin)" tCount
}

But for the tertiary sort the secondary sort is unnecessary, since the execution of the query is forced into single-threaded mode by any number of factors. But if we wish to sort intra-series (who would do such a thing?), then we need to bind the series together with that secondary sort. For sanity's sake when examining the results, we recommend commenting out all but the primary sort.

The easy stuff

Some of the examples below will include the variations parameter in the CQL header, the cross-twin pattern expressing across full solution trees. For those examples, an understanding of game tree traversal can be helpful in deciphering the operation of the query. A companion document provides a starting point toward that end, with link provided at the end of this document.

The striptease
We'll start out with something simple — almost trivial — as we demonstrate the novel striptease twinning theme. Twins are produced simply by stripping pieces (all of the same color) off the board. The starting position for each twin in the series is a continuation from the last.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent wCount = #A
  persistent bCount = #a
  if TwinCount < 4 then SeriesAbort = 1
  false
} else {
  if #A < wCount and #a == bCount
    then wCount = #A
    else SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Besides stipulating that the white piece count decreases with each successive position, we also require that the black piece count remains unchanged. If the test fails at any point in the series, we set an abort flag to waive off the match.
We also give a lower bound on the number of twins in the striptease series. A striptease of one (or even two or three) is not likely to be terribly interesting.

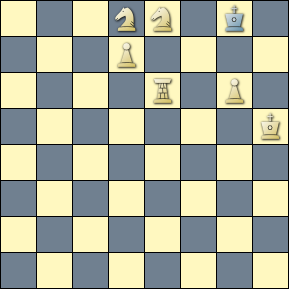
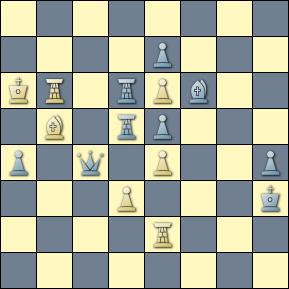
The query matches the following composition by Bidleň, with the board finally stripped down to just kings and a single pawn threatening to promote. This is a fairly simple composition to solve with only a few pieces on the board, but many of the matching series are quite challenging and can become even moreso as the pieces are stripped away.

[Event "Comm., SuperProblem, TT-133"]
[Site "Yet Another CPDB"]
[Date "2015.03.27"]
[Round "12602800"]
[White "Bidleň, Anton"]
[Black "#2 -- Twins -- Actual+Virtual Play"]
[Result "1-0"]
[BlackElo "4"]
[Keywords "Striptease"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#2"]
[TwinB "Remove e8"]
[TwinC "Cont Remove e6"]
[TwinD "Cont Remove d8"]
[TwinE "Cont Remove g6"]
[FEN "3NN1k1/3P4/4R1P1/7K/8/8/8/8 w - - 0 1"]

a) 

   1.Re6-f6 ! zugzwang.
      1...Kg8-h8
          2.Rf6-f8 #


b) -wSe8  

   1.Kh5-h6 ! threat:
          2.Re6-e8 #


+c) -wRe6  

   1.Sd8-e6 ! threat:
          2.d7-d8=Q #
          2.d7-d8=R #


+d) -wSd8  

   1.Kh5-h6 ! threat:
          2.d7-d8=Q #
          2.d7-d8=R #
      1...Kg8-f8
          2.d7-d8=Q #


+e) -wPg6  

   1.Kh5-g6 ! threat:
          2.d7-d8=Q #
          2.d7-d8=R #
      1...Kg8-f8
          2.d7-d8=Q #

Forsberg twins
If we replace the piece occupying a single square of the base starting position with a piece of the same color across every twin in the series, we have a Forsberg series. If, over the series, every possible piece (save the king) is substituted for the original, then we have a full Forsberg series.
Our approach for the query is fairly simple. If the board is unchanged across the series but for the one piece, then the respective FEN strings will be identical but for the one character. If the string index for that character is the same for every twin across the series, then we have a match.

// Forsberg twins.  (CQLv6.2)
cql(quiet)
initial

function deltaFEN(FEN1 FEN2) {
  Index = #FEN1 - 1
  while (Index ≥ 0) {
    if FEN1[Index] ≠ FEN2[Index]
      if Deltas[Index]
        then Deltas[Index] = Deltas[Index] + FEN2[Index]
        else Deltas[Index] = FEN1[Index] + FEN2[Index]
    Index -= 1
  }
}

function isMatch(PT) {
  #Deltas == 1
  Match = 1
  Key ∊ Deltas {
    if #PT ≠ #(Deltas[Key]) then Match = 0
    while (PT ~~ ".")
      if not \0 in Deltas[Key] then Match = 0
  }
  Match == 1
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Occupied = ◭
  persistent FEN = fen ~~ "^[^ ]+"
  dictionary Deltas[0] = "0"  unbind Deltas
  false
} else {
  if Occupied == ◭
    then deltaFEN(FEN  fen ~~ "^[^ ]+")
    else SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and (isMatch("QRBNP") or isMatch("rbn"))
    then true
    else false
}

If we have a Forsberg, the dictionary carrying the substitution data will have but one entry. We allow that one might wish to look for a Forsberg that substitutes a specific set of pieces, white or black. The information collected for each twin gives us that set.
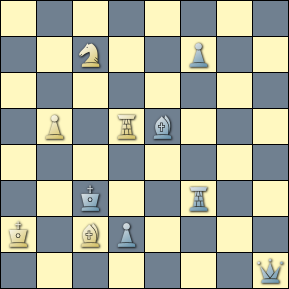
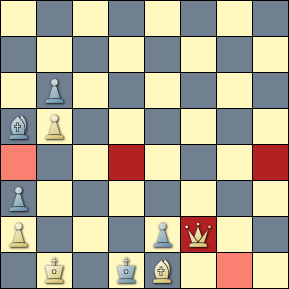
The query matches the following helpmate by Abdurahmanović, in which the white queen at c7 is traded out for every other piece type in the inventory.

Note the extended star pattern across the respective solutions that is traced by the black king. It is not uncommon for patterns or themes to express (independently) across both starting positions and solutions. This particular composition is well-deserving of its awarded 1st Prize.

[Event "1st Prize, Schach-Echo"]
[Site "Yet Another CPDB"]
[Date "1973.??.??"]
[Round "10336300"]
[White "Abdurahmanović, Fadil"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "4"]
[Keywords "Forsberg twins:Star Black King"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Add white Rc7"]
[TwinC "Add white Bc7"]
[TwinD "Add white Sc7"]
[TwinE "Add white Pc7"]
[FEN "q7/nbQ4R/p5p1/1p4p1/3k4/8/p1ppp2K/1rn1b3 b - - 0 1"]


a) 

  1.Bb7-e4 Rh7-h3   2.Qa8-d5 Qc7-c3 #

b) wRc7  

  1.Kd4-e5 Rc7-e7 +   2.Ke5-f6 Rh7-f7 #

c) wBc7  

  1.Kd4-c3 Rh7-h3 +   2.Kc3-b2 Bc7-e5 #

d) wSc7  

  1.Kd4-e3 Sc7-d5 +   2.Ke3-f2 Rh7-f7 #

e) wPc7  

  1.Kd4-c5 c7-c8=Q +   2.Kc5-b6 Qc8-c7 #

If we extend the pattern and apply the same substitutions simultaneously across multiple squares, then we have a Forsberg-Andersson theme. Typically, the parallel substitutions involve just the rook, bishop and knight across the series. The substitutions are color for color and must be consistent across the series, though they may include substitutions for both colors in any given position.
The query is a bit more involved than what we saw for the plain vanilla Forsberg, which was fairly limited in its variability. The matching series tend to be more striking in their originality and difficulty, and are therefore more or less worthy of the extra work (or so we remind ourselves constantly).

// Forsberg-Andersson twins.  (CQLv6.2)
cql(quiet)
initial

function isForsberg(FEN1 FEN2) {
  deltaType = ""  Affirm = 1
  Index = #FEN1 - 1
  while (Index ≥ 0) {
    if FEN1[Index] ≠ FEN2[Index] {
      // All subs per twin must be color for color (no kings).
      if not (FEN1[Index] in "QRBNP" and FEN2[Index] in "QRBNP" or
              FEN1[Index] in "qrbnp" and FEN2[Index] in "qrbnp")
        then Affirm = 0
      // All subs per twin must be of the same piece type.
      if deltaType == ""
        then deltaType = uppercase FEN2[Index]
        else if deltaType[0] == uppercase FEN2[Index]
               then deltaType += uppercase FEN2[Index]
               else Affirm = 0
      // Finally, record all substituted (+original) types per "square".
      if Deltas[Index]
        then Deltas[Index] = Deltas[Index] + FEN2[Index]
        else Deltas[Index] = FEN1[Index] + FEN2[Index]
    }
    Index -= 1
  }
  Affirm == 1 and #deltaType > 1 // more than one substitution
}

function isMatch(PT) {
  Match = 1
  Key ∊ Deltas
    while (PT ~~ ".")
      if not uppercase \0 in uppercase Deltas[Key] then Match = 0
  Match == 1
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Occupied = ◭
  persistent FEN = fen ~~ "^[^ ]+"
  dictionary Deltas[0] = "0"  unbind Deltas
  false
} else {
  if Occupied ≠ ◭
    then SeriesAbort = 1
    else if not isForsberg(FEN  fen ~~ "^[^ ]+") then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and #Deltas ≥ 3  // the number of Forsbergs (squares) per twin
      and isMatch("RB") // case insensitive and the types given are a minimum
    then true
    else false
}

In stipulating the match criteria we allow ourselves two controls: 1) a range in the number of substitutions per twin, and 2) a selection of the piece types comprising the Forsberg-Andersson (as a minimum). Set the controls to 2 and a null string, respectively, to pick up pretty much anything even resembling an F-A.
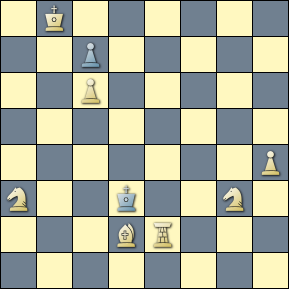
The query as given matches the following helpmate by Valtonen, in which bishops and rooks are substituted for the knights across a 3-series. Note that the promotion for each solution is respective of the substitution applied to the twin. A very nice composition.

[Event "1st Prize, Sakkélet"]
[Site "Yet Another CPDB"]
[Date "1989.??.??"]
[Round "10834000"]
[White "Valtonen, Kari"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "2"]
[Keywords "Forsberg-Andersson theme:Twin substitute"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Substitute S B"]
[TwinC "Substitute S R"]
[FEN "2r5/8/5q2/8/2NNp3/7p/1n1p4/3k2K1 b - - 0 1"]


a) 

  1.Kd1-c1 Sc4-a3   2.d2-d1=S Sd4-b3 #

b) S ==> B  

  1.Kd1-c1 Bc4-d3   2.d2-d1=B Bd4-e3 #

c) S ==> R  

  1.Kd1-e1 Rc4-c2   2.d2-d1=R Rd4*e4 #

Exchange cycles
A piece (the same piece) exchanges places with some piece of the opposing side across each twin of the series. The board is otherwise unchanged. The pattern carries through at least two twins, else it's not of much interest.
We could revise this example with an approach similar to the Forsberg example above, but frankly we rather like the discovery that comes with the imprecision below. And what is to be learned from repeating the technique, anyways? We'll leave it alone and move on to some new things.

cql(include libcql/libhlp.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $wOccupied = A
  persistent $bOccupied = a
  persistent $prevExchange = [Aa]
  if TwinCount < 2 then SeriesAbort = 1
  false
} else {
  Exchange = XOR($wOccupied A) | XOR($bOccupied a)
  if XOR($wOccupied A) != 2 or XOR($bOccupied a) != 2 or
      Exchange != 2 or Exchange & $prevExchange == 0
    then SeriesAbort = 1
  $prevExchange = Exchange
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The test for the pattern is, perhaps, not so obvious. It's not enough to know that two occupied squares have changed, but that they have changed for a piece of both colors. We also check that one of those squares was involved in the previous exchange, which is a little bit imprecise but is good enough.
Often, the exchange cycle is indicative of other thematic cycles at play. The following matching helpmate by Schurawljow is an example.

[Event "2nd Comm., Шахматная поэзия"]
[Site "Yet Another CPDB"]
[Date "2007.??.??"]
[Round "11981400"]
[White "Schurawljow, Andrej Nikolajewitsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "2"]
[Keywords "Annihilation:Cycle of squares:Cycle of functions of white pieces"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Exchange e4 d4"]
[TwinC "Exchange e4 f3"]
[FEN "bB3RK1/p2p4/8/8/q2PpNRn/4kPp1/3p1p2/3n4 b - - 0 1"]


a) 

  1.Sh4*f3 Bb8*a7   2.Sf3*d4 Rg4*g3 #

b) bPe4<-->wPd4  

  1.Ba8*e4 Rg4*g3   2.Be4*f3 Rf8-e8 #

c) bPe4<-->wPf3  

  1.Qa4*d4 Rf8-e8   2.Qd4*e4 Bb8*a7 #

We'll show one more matching composition, where we double up on the exchange cycle in a pattern expressed between four rooks. This would be another of those serendipitous finds, a result of the slight imprecision in the query.
We find something very appealing about this helpmate.

[Event "Special Prize, SuperProblem"]
[Site "Yet Another CPDB"]
[Date "2018.02.18"]
[Round "12750100"]
[White "Lind, Ingemar"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "4"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Exchange e5 e6"]
[TwinC "Exchange e6 f6"]
[TwinD "Exchange f6 f5"]
[TwinE "Exchange f5 e5"]
[FEN "3bb3/2p5/4rR2/4Rr2/6k1/4p3/4K2n/6q1 b - - 0 1"]


a) 

  1.Kg4-h3 Rf6-g6   2.Rf5-f6 Re5-h5 #

b) wRe5<-->bRe6  

  1.Rf5-h5 Rf6-f3   2.Re5-g5 Re6-e4 #

c) bRe6<-->wRf6  

  1.Kg4-f4 Re5*e3   2.Qg1-g5 Re6-e4 #

d) wRf6<-->bRf5  

  1.Re6-e7 Rf5-h5   2.Rf6-f4 Re5-g5 #

e) bRf5<-->wRe5  

  1.Be8-h5 Rf5-f3   2.Re5-g5 Rf6-f4 #

The Igman theme
The definition of the Igman is apparently a closely held secret within the community. The google-net knows nothing of it and we can find only two examples of it anywhere that actually refer to the theme by name. Thus, we surmise, without prejudice and with very little evidence, that the theme is open to interpretation.
As best we can determine, at the crux of the theme is the proposition that every one of the mating pieces across the series changes its color at some point across the series, and not in any particular order. There is at least a hint that the theme is intended for rooks, bishops and knights only, and that all of those pieces must be and only those pieces may be represented in the pattern (though we have found some exceptions that look suspiciously like Igmans in spirit).

And — just because we can — we'll also stipulate that 1) the twin specifications across the series are not necessarily restricted to the one thematic change per twin, and 2) the one class of composition for which the theme is most likely applicable is the helpmate.

Even though we have had to invent the definition, we rather like the theme and feel it is worthy of consideration. It weaves solution with initial position across the series in a way that seems to be at least relatively unique in our limited experience with the twinning domain. And it requires a slightly different language technique in deriving the query.

Because the color exchanges must be piece type for piece type, we feel compelled to cast off our usual casual approach and employ a number of bitboards at their finest achievable granularity. We find that act of desperation distasteful, but there you have it.

cql(include libcql/libhlp.cql quiet)
initial

function Mater() { find {terminal  piece M = move to . previous}  M }
function cxSquares() { $R & r | $B & b | $N & n }

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $R = R
  persistent $B = B
  persistent $N = N
  persistent Igmans = []
  persistent Maters = Mater()
  if not isHelp() or isDual() then SeriesAbort = 1
  false
} else {
  if not isHelp() or isDual() then SeriesAbort = 1
  Maters |= Mater()
  Igmans |= cxSquares()
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and
      #($R|$B|$N) == #Maters and Maters in Igmans
    then {
      //message("Maters:" Maters " Igmans:" Igmans)
      true
    } else false
}

The set of mating pieces correlates with pieces as they are arranged in the initial position of the base board. The Mater() function first acquires the piece id of the solution's mating piece in the context of the terminal position, and then returns the square occupied by that piece in the context of the initial position of the respective twin. Note that we collect all mating pieces across the series, whether qualifying as Igman candidates or not.
We also collect the set of color exchange candidates that have actually fulfilled their obligation. The cxSquares() function builds that set, which includes every candidate that has changed color versus the base position.

Up until end-of-series, we have established no correlation between solution and initial position. We've simply collected the relevant data from each of the twins in the series. The series match is conditioned on two things: 1) that the number of mating pieces is equal to the number of candidates registered in the base position, and 2) that the set of mating pieces is a subset of the set of color-changing Igmans. We do not adhere to the all/must and only/may principle outlined above, as the Igman set as determined by the query above may comprise, e.g., a rook and two bishops.

The following composition demonstrates the Igman theme with one each of the candidate piece types on the board. The knight mates twice, giving us the consummate Igman.

[Event "Special Prize, Probleemblad"]
[Site "Yet Another CPDB"]
[Date "1993.??.??"]
[Round "11005600"]
[White "Bakcsi, György & Zoltán, László"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "3"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Add black Rd5"]
[TwinC "Add black Bc2"]
[TwinD "Add black Sc7"]
[FEN "8/2N2p2/8/1P1Rb3/8/2k2r2/K1Bp4/7q b - - 0 1"]


a) 

  1.Kc3-c4 Sc7-a6   2.Be5-c3 Bc2-b3 #

b) bRd5  

  1.Rd5-d3 Bc2-b3   2.Be5-d4 Sc7-d5 #

c) bBc2  

  1.Qh1-f1 Rd5-d4   2.Qf1*b5 Sc7*b5 #

d) bSc7  

  1.Sc7-e6 Ka2-a3   2.Se6-d4 Rd5-c5 #

The star-cross crapshoot
We have from time to time been accused (so unfairly) of engaging in hyperbole as we lavish praise on the v6.1 release of the language. In defense of lavishness, let us offer up this example as case in point. We preserve the pre-6.1 queries and tack on the post-6.1 revision at the tail end so that the jury may engage in a compare'n'contrast exercise of their own.

Stunning. Unbelievable. Mind-blowing. These are the words that have been whispered about the public square. Okay, so we employ the occasional superlative. But before ye mock us, read on fair pilgrim and decide for yourself.

CQLv6.0 original version

We often will see a thematic star-flight or cross-flight pattern expressed across solution phases, and one will come across plenty of that in a twinning context as well. But what we're after here is the detection of such patterns that are expressed across twins, and that are not limited to the kings.

Typically, such patterns will express across twins at the same ply in the solution for any given piece, with multiple patterns expressing across a series at multiple ply. But we might also find the pattern realized across different ply across twins for a given piece, especially for the longer length classes of composition.

Taking all the possible combinations/permutations of the elements into consideration, the construction of a query in search of multiple such patterns across a single series can be a daunting undertaking, and is likely to result in a perversion of the language. In fact, we have very little idea what we're looking for in terms of the number of patterns expressed, the types of patterns (star or cross), the piece type stepping through the pattern, or the plies across which the patterns are realized. What to do?

Though we might not know the details of how the pattern is realized, we do know what the end product should look like. If we were to collect in a single bitboard all of the moves made (destination squares) across all of the solutions of the series, could we still distinguish the patterns from all of the noise? We thought it unlikely enough — though nonetheless intriguing and challenging — that we should go ahead and roll the dice.

There are some things that we can do to improve our odds:
1. Break up the single bitboard into two, one for the odd ply and one for the even. This segregates the patterns by side-to-move, and so patterns are kept intact by piece.
2. Limit the square-gathering to moves by pieces that are actually candidates for expressing the pattern (i.e., no pawns, no knights).
3. Limit the number of moves for which we collect squares, without limiting the extent of the stipulation.
We also know a couple of things about the twin series across which these patterns will be found: 1) unlike intra-solution patterns of this type, inter-solution patterns are limited to the helpmate class, and 2) we know that the patterns we're interested in are expressed across a 4-series only.

The following query implements the search described above, matching a series which expresses some minimal number of star and/or cross patterns across twins, taking into consideration the first two moves (each side) of every solution in the series. We sort the matching series by the number of patterns detected.

cql(quiet)
initial  btm

function byColor(bb) {
  line singlecolor --> .{0 1} --> bb = bb | move to . from [KkQqBbRr]
}

function vSquares(odd even) {
  line --> byColor(odd) --> byColor(even)
}

function scCount(odd even) {
  (shift count {(diagonal 1 b2) & odd == 4}) +
  (shift count {(diagonal 1 b2) & even == 4}) +
  (shift count {(orthogonal 1 b2) & odd == 4}) +
  (shift count {(orthogonal 1 b2) & even == 4})
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $Odd = ~.
  persistent $Even = ~.
  if TwinCount != 3 then SeriesAbort = 1
  vSquares($Odd $Even)
  false
} else {
  vSquares($Odd $Even)
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and
      sort "Star+Cross" scCount($Odd $Even) > 1
    then {
      // message($Odd $Even " " scCount($Odd $Even))
      true
    } else false
}

Given the constraints set by the query, each of the pattern-carrying bitboards will max out at cardinality of eight and the number of patterns per series will max out at four. A count greater than four indicates some number of false positives.

The two functions vSquares() and byColor() effectively give us a pair of nested line filters, one for the odd ply and one for the even. The regex repetition factor repeats for the first two moves of the line for a given color.

Note that — due to precedence rules — the grouping that we see in the scCount() function is necessary. Without it, the CQL engine will wander off into a deep dark non-linear hole gobbling up system resources. Having discovered this the hard way (we're still not sure what we unleashed), we thought it prudent to adjust the default parameters by which the Linux kernel decides that a process is runaway (see the ulimit shell command). We mention this only as a heads up for those interested in experimenting with or modifying the query.

The composition by Bulauka delivers a cross pattern and three star patterns across a 4-series, all in 4 ply. The white pieces step through their respective patterns across the same ply, the black pieces swapping ply. The two kings shadow one another across solutions, as if in something of a cooperating dance (which, of course, is the essence of a helpmate).

[Event "1st Prize, Wola Gułowska"]
[Site "Yet Another CPDB"]
[Date "2005.05.15"]
[Round "11856500"]
[White "Bulauka, Aljaksandr Genadsewitsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "3"]
[Keywords "BB star:WK star:BK star:WR cross:Task"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Move d6 h3"]
[TwinC "Move f7 b2"]
[TwinD "Move b1 e3"]
[FEN "3Nb3/3q1n2/2PpP3/4b3/rrp1kPK1/6PP/2Rppp2/1B6 b - - 0 1"]


a) 

  1.Be5-f6 Kg4-h5   2.Ke4-f5 Rc2-b2 #

b) -wPh3  bPd6-->h3  

  1.Be5-d6 Kg4*h3   2.Ke4-f3 Rc2-c3 #

c) bSf7-->b2  

  1.Ke4-d3 Kg4-f3   2.Be5-d4 Rc2-c1 #

d) wBb1-->e3  

  1.Ke4-d5 Kg4-f5   2.Be5*f4 Rc2*d2 #

In examining a fair sample of the matching series, it's clear that the accuracy of the query is less than one would like. We could improve it by registering moves across odd/even ply by piece type, but we would then have to redefine the term tedious.
Rather than gathering moves in a dedicated bitboard for every piece type — and just to make our point — we'll adjust the query to separate out kings from the rest of the pack, the king pattern being ubiquitously present amongst the many series that we're looking to match and thus likely to have the greatest impact on the result.

cql(quiet)
initial  btm

function byColor(bb pt) {
  line singlecolor --> .* --> bb = bb | move to . from pt
}

function vSquares(odd even pt) {
  line --> byColor(odd pt) --> byColor(even pt)
}

function scCount(odd even) {
  (shift count {(diagonal 1 b2) & odd == 4}) +
  (shift count {(diagonal 1 b2) & even == 4}) +
  (shift count {(orthogonal 1 b2) & odd == 4}) +
  (shift count {(orthogonal 1 b2) & even == 4})
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $OddK = ~.
  persistent $EvenK = ~.
  persistent $Odd = ~.
  persistent $Even = ~.
  if TwinCount != 3 then SeriesAbort = 1
  vSquares($OddK $EvenK [Kk])
  vSquares($Odd $Even [QqRrBb])
  false
} else {
  vSquares($OddK $EvenK [Kk])
  vSquares($Odd $Even [QqRrBb])
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and
      (sort "Star+Cross Kings" scCount($OddK $EvenK)) > 0 and
      (sort "Other" scCount($Odd $Even)) > 0
    then {
      //message($OddK $EvenK " " scCount($OddK $EvenK) " " $Odd $Even " " scCount($Odd $Even))
      true
    } else false
}

As the query is given, we expect at least one king pattern and at least one pattern from an other piece type. We can adjust those conditions to search for any combination of patterns that we like. We could also adjust the piece designators passed to the vSquares() function to narrow the search to, e.g., only kings and queens.
Note that the separation of just the kings from the rest of the pack is so effective that we no longer need to restrict square-gathering (the byColor() function) to the first two moves of the solution. We're now gathering moves for the entire length of the solution.

The following helpmate-in-three by Abdurahmanović demonstrates just how crazy one can get with this theme. Both kings and all three bishops on the board step their way through their respective star patterns, in some cases crossing all three of their ply in the process.

The query is still not perfect, but as this composition and the entire field of matching series demonstrate, it is far more accurate than was our first attempt.

[Event "Schach-Echo"]
[Site "Yet Another CPDB"]
[Date "1978.04.??"]
[Round "10458600"]
[White "Abdurahmanović, Fadil"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "3"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move a8 b2"]
[TwinC "Move d4 h6"]
[TwinD "Move d4 h4"]
[FEN "q7/8/2p1bb2/3BPk2/r2p1p2/5K2/8/3n4 b - - 0 1"]


a) 

  1.Bf6*e5 Bd5-c4   2.Be6-d5 + Kf3-e2   3.Kf5-e4 Bc4-d3 #

b) bQa8-->b2  

  1.Be6-d7 Bd5*c6   2.Kf5-e6 Kf3-e4   3.Bf6-e7 Bc6-d5 #

c) bPd4-->h6  

  1.Be6-f7 Bd5-e6 +   2.Kf5-g6 Kf3-g4   3.Bf6-g7 Be6-f5 #

d) bPd4-->h4  

  1.Bf6-g5 Kf3-g2   2.Kf5-g4 Bd5-e4   3.Be6-f5 Be4-f3 #

We should probably point out a thing or two regarding flow of execution (evaluation) within a cross-twin query. In general, the flow requires that a failure in evaluation of one filter should not abort the evaluation of follow-on filters in a compound, the flow more-or-less relying on its completion.
Of particular consequence with the query above is the vSquares() function, which we would like to always evaluate as true. By extension, for all to work reliably, the byColor() function should always evaluate as true. Looking things over, we decide that everything is in order, since an assignment to a set variable always matches the current position.

But there's a catch. If there is no game tree, then the line filter fails. As we've noted elsewhere in this document, a zeroposition has no solution and thus no game tree. Now, since a zeroposition is always the base position in the series, this only has an impact on the then clause of the outer if-then-else construct, and can therefore be handled gracefully (since that clause is intended to always fail). Nevertheless, this is an issue that one should be aware of when CQL'ing in the twinning domain.

CQLv6.1 revision

The problem with the original approach is that we had to rely on the gods of chance to raise the pattern above all of the noise on the board. Working around that problem would have entailed mind-numbing monotony.

Not so with the 6.1 release. First class strings and the all-purpose dictionary allow us to cancel out the noise without breaking a sweat. The revision is not only far simpler and easier to understand, it is perfectly accurate in its results. All the credit goes to the CQL developers, who really thought through the critical details of the release.

// The star-cross crapshoot.  (CQLv6.2)
cql(include libcql/libhlp.cql quiet)
initial

function RecordMoves() {
  if child  // don't fail on zeroposition
    line
      --> {
          not terminal
          piece Piece = move from ▦
          PKey = str(Piece)
          if Moves[PKey]
            then Moves[PKey] = Moves[PKey] ∪ move to ▦
            else Moves[PKey] = move to ▦
          }{*}
}

function Countem(PT) {
  Count = 0
  Key ∊ Moves
    if Key[0] in PT
      if (shift {(diagonal 1 b2) ∩ Moves[Key] == 4}) or
         (shift {(orthogonal 1 b2) ∩ Moves[Key] == 4})
        then Count += 1
  Count
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  dictionary Moves[""] = []  unbind Moves
  RecordMoves()
  if not isHelp() or isDual() then SeriesAbort = 1
  if not (TwinCount == 3 or TwinCount == 4 and tag "TwinA")
    then SeriesAbort = 1
  false
} else {
  if not isHelp() or isDual() then SeriesAbort = 1
  RecordMoves()
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      //and Countem("KQRBkqrb") > 0
      and Countem("Kk") > 1
      and Countem("Bb") > 2
    then {
      //message(Moves)
      true
    } else false
}

We make allowance for a zeroposition series with this example, having accidentally noticed that we had a few in the database that qualified. We also allow some flexibility in stipulating the piece types that participate in the pattern. It's worth taking the time to play around with that a little bit.

Wheeling knights
Rather than wheeling across initial positions in a series (a pattern we have never seen as a complete wheel), we typically have a knight wheeling across solutions. Each spoke of the wheel then serves either as the key to the respective twin's solution or as the mating move in actual play.
Tackling the key-serving wheel first, we'll employ persistent set variables 1) to uniquely identify the wheeling knight in the base position in case there are multiple knights on the board, and 2) to register spokes in the wheel as they are visited so that we can finally test that all the spokes are accounted for in the end.

The query is structured for two passes so that we can sort the results by the number of spokes in the wheel, and while we're at it we fill out the matching series on the second pass.

// Wheeling knights.  (CQLv6.2)
cql(quiet)
initial

if isunbound DryRun then DryRun = 1  // zero for wet run
if isunbound FD then FD = "/tmp/out.cqo"

if (DryRun == 0 and gamenumber == 1) {
  dictionary Series
  SeqNums = readfile FD
  while (SeqNums ~~ "(.+):(.*)")  Series[\1[:6]] = int(\2)
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent TC = TwinCount + 1
  persistent Spokes = move to ▦ from ♘♞
  persistent Wheeler = move from ♘♞
  DryRun == 0 and Series[(tag "SeqNum")[:6]]
} else {
  if move from ♘♞ ∩ Wheeler then Spokes ∪= move to ▦
  TwinCount -= 1
  if DryRun == 1
    then if TwinCount == 0 and TC == Spokes ≥ 4
      then writefile(FD str(tag "SeqNum" ":" #Spokes \n))
      else false
    else Series[(tag "SeqNum")[:6]]
}

if DryRun == 0
  sort "Spokes" Series[(tag "SeqNum")[:6]]

Series with a full wheel will move to the top of the results. Note that the Wheeler must necessarily be a knight visiting the first spoke in the wheel in the base position, else all bets are off.
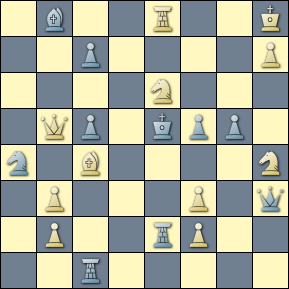
The query matches a composition by Stojnic which expresses one theme stacked upon another across solutions. For every spoke in the white knight's wheel (the key for the respective twin) the black king steps through his star flight, awaiting mate at every turn.

[Event "The Problemist"]
[Site "Yet Another CPDB"]
[Date "2010.??.??"]
[Round "12214100"]
[White "Stojnic, Dragan"]
[Black "#2 -- Twins -- Actual+Virtual Play"]
[Result "1-0"]
[BlackElo "7"]
[Keywords "WS wheel"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#2"]
[TwinB "Move e8 e7"]
[TwinC "Move b3 d6"]
[TwinD "Move h7 g6"]
[TwinE "Move c7 e4"]
[TwinF "Move f2 d7"]
[TwinG "Move f2 f7"]
[TwinH "Move c4 d5"]
[FEN "1b2R2K/2p4P/4N3/1Qp1kpp1/n1B4N/1P3P1q/1P2rP2/2r5 w - - 0 1"]


a) 

   1.Se6-f8 + !
      1...Ke5-d4
          2.Qb5-d7 #
      1...Ke5-f4
          2.Sf8-g6 #
      1...Ke5-f6
          2.Sf8-d7 #
      1...Ke5-d6
          2.Qb5-d7 #


b) wRe8-->e7  

   1.Se6*c7 + !
      1...Ke5-d4
          2.Qb5-d7 #
      1...Ke5-f4
          2.Sc7-d5 #
      1...Ke5-f6
          2.Sc7-d5 #
      1...Ke5-d6
          2.Qb5-d7 #


c) wPb3-->d6  

   1.Se6*c5 + !
      1...Ke5-d4
          2.Sc5-b3 #
      1...Ke5-f4
          2.Sc5-d3 #
      1...Ke5-f6
          2.Sc5-d7 #
      1...Ke5*d6
          2.Sc5-b7 #


d) wPh7-->g6  

   1.Se6*g5 + !
      1...Ke5-d4
          2.Qb5-d7 #
      1...Ke5-f4
          2.Sg5*h3 #
      1...Ke5-f6
          2.Sg5-h7 #
      1...Ke5-d6
          2.Sg5-f7 #


e) bPc7-->e4  

   1.Se6-d8 + !
      1...Ke5-d4
          2.Sd8-c6 #
      1...Ke5-f4
          2.Qb5*b8 #
      1...Ke5-f6
          2.Re8-e6 #
      1...Ke5-d6
          2.Qb5-c6 #


f) wPf2-->d7  

   1.Se6-g7 + !
      1...Ke5-d4
          2.d7-d8=Q #
          2.d7-d8=R #
      1...Ke5-f4
          2.Sg7-h5 #
      1...Ke5-f6
          2.Sg7-h5 #
      1...Ke5-d6
          2.d7-d8=Q #
          2.d7-d8=R #


g) wPf2-->f7  

   1.Se6-d4 + !
      1...Ke5*d4
          2.Qb5-d7 #
      1...Ke5-f4
          2.Sd4*e2 #
      1...Ke5-f6
          2.f7-f8=Q #
          2.f7-f8=R #
      1...Ke5-d6
          2.Qb5-c6 #


h) wBc4-->d5  

   1.Se6-f4 + !
      1...Ke5-d4
          2.Qb5-d3 #
      1...Ke5*f4
          2.Sh4-g6 #
      1...Ke5-f6
          2.Sf4-h5 #
      1...Ke5-d6
          2.Qb5-c6 #

When the wheeling pattern expresses across mating moves in actual play, we have a whole different beast. Different, in part, because the variations parameter is given in the CQL header. But we also must take into account that, at the extremities of the solution trees, there's alot of noise that we'll want to filter out.
As we did with the query above, we'll allow for other than an inflexible eight-count on the number of spokes on the wheel. Below, we also want to match lesser wheels which are the consequence of a knight wheeling from on or near an edge of the board. But even for those lesser wheels, we want the pattern to include all spokes that are legal from the square occupied by the knight.

We're looking for "pure" patterns, where the knight moves are the only mating moves. We'll also eliminate solutions with duals, as those are invariably mates by discovery as the knight wheels its way out of the line of attack.

cql(quiet variations)
initial

function FindLegalWheel() {
  find {
    terminal
    ancestor(position 1  currentposition)
    not find <-- move null previous
  }:{flip up 2 right 1 (move from [Nn] previous)}
}

function FindSpokes() {
  spokes = []
  line
    --> move primary
    --> {not move null}*
    --> {
        terminal
        if move from [Nn] previous and depth == parent:depth
          then spokes |= move to . previous
          else SeriesAbort = 1
        }
  spokes
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent LegalWheel = FindLegalWheel()
  persistent Spokes = FindSpokes()
  false
} else {
  Spokes |= FindSpokes()
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and
       Spokes == LegalWheel and Spokes >= 4
    then true
    else false
}

The FindLegalWheel() function gives us the set of legal moves (squares) available to the knight. In identifying the wheeling knight, we eliminate threat lines from consideration and accept the first knight encountered in actual play. If the first qualifying position for the find filter is not the result of a knight move, then the legal wheel will be an empty set and the twin series will fail to match. Note that we could have used a move filter with the legal parameter, but that would not have included squares occupied by friendly pieces which might have been captured at some point in the solution.
The FindSpokes() function returns the set of squares representing mating moves by knights in actual play. There may be more than one for other than a help mate. The condition depth == parent:depth catches duals and will abort the match on the series.

The query matches the helpmate below, which, incidentally, gives us a pair of knights wheeling their way across twins (as if one were not challenge enough).

[Event "1st-2nd Prize, ЮК В.Чепижный-70 (h#2)"]
[Site "Yet Another CPDB"]
[Date "2004.??.??"]
[Round "11737900"]
[White "Michailowski, Igor Anatoljewitsch & Nefjodow, Wladislaw Walerjewitsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "7"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Move f6 g7"]
[TwinC "Cont Move h7 h1"]
[TwinD "Cont Move g7 h4"]
[TwinE "Cont Move h1 b3"]
[TwinF "Cont Move b4 a2"]
[TwinG "Cont Move b3 b7"]
[TwinH "Cont Move c7 b6"]
[FEN "8/n1r2p1k/5q1r/1P2NP1p/1p2NKpp/5Pp1/2p3b1/n7 b - - 0 1"]


a) 

  1.Rh6-g6 Se5*f7   2.Rg6-g7 Se4*f6 #

b) bQf6-->g7  

  1.Rc7-c8 Se5-g6   2.Rc8-g8 Se4-g5 #

+c) bKh7-->h1  

  1.Bg2*f3 Se5*f3   2.g3-g2 Se4-f2 #

+d) -bPh4  bQg7-->h4  

  1.Qh4-h2 Se5*g4   2.Qh2-g1 Se4*g3 #

+e) bKh1-->b3  

  1.Kb3-a2 Se5-c4   2.b4-b3 Se4-c3 #

+f) bPb4-->a2  

  1.Kb3-b2 Se5-d3 +   2.Kb2-b1 Se4-d2 #

+g) bKb3-->b7  

  1.Rh6-h8 Se5-d7   2.Rh8-a8 Se4-d6 #

+h) bRc7-->b6  

  1.Sa7*b5 Se5-c6   2.Kb7-a6 Se4-c5 #

The Polish
The Polish theme is a board-wide color exchange. The query is so completely trivial that it is hardly worth bothering with, except that it plays into the next example (the king exchange).

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent White = A
  persistent Black = a
  false
} else {
  if White != a or Black != A then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The test we use for the color exchange is that — post-exchange — the occupied square sets for the white and black pieces have swapped. True, this is an pattern approximation (sans piece type), but every one of the 170+ matching series is a Polish.
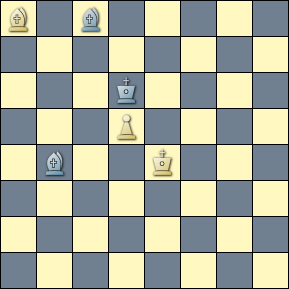
One of those matches is the following helpmate by Tura, where a Chameleon Echo is expressed across twin solutions. Let that sink in for a minute. The Chameleon pattern expresses across twin compositions after a board-wide color exchange.

[Event "1st Prize, Wola Gułowska"]
[Site "Yet Another CPDB"]
[Date "1988.??.??"]
[Round "10799700"]
[White "Tura, Waldemar"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Chameleon echo mates:Ideal mates"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "PolishType"]
[FEN "B1b5/8/3k4/3P4/1b2K3/8/8/8 b - - 0 1"]


a) 

  1.Kd6-d7 d5-d6   2.Bb4-a5 Ke4-d5   3.Ba5-d8 Ba8-c6 #

b) PolishType  

  1.d5-d4 Kd6-e7   2.Ke4-e5 Bc8-e6   3.Ba8-e4 Bb4-d6 #

The king exchange
Here we have what amounts to another color exchange, this one applied only to the kings. That the kings exchange colors is a necessary criterion, but it is nowhere near sufficient as we would pick up hundreds of Polish twins as well (see the previous example). We should also establish that the rest of the board remains unchanged.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent White = A & ~K
  persistent Black = a & ~k
  persistent wK = K
  persistent bK = k
  false
} else {
  if wK != k or bK != K or White != [QRBNP] or Black != [qrbnp]
    then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Again we leave the query at an approximation, ignoring piece type (but for the kings) and testing only that sets of white and black occupied squares hold constant. At this point, we should not be surprised that approximation works well enough.
The query matches the following composition by a trio of composers, in which a mixed Allumwandlung is realized across twin solutions after the exchange of kings.

[Event "Special Prize, Lebedkin MT"]
[Site "Yet Another CPDB"]
[Date "1996.??.??"]
[Round "11156800"]
[White "Selivanov, Andrey Vladimirovich & Kralin, Nikolai Iwanowitsch & Perwakow, Oleg Wiktorowitsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Allumwandlung"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Exchange a2 a4"]
[FEN "8/P7/8/n7/k7/N7/K3p3/8 b - - 0 1"]


a) 

  1.e2-e1=B a7-a8=S   2.Be1-b4 Sa8-b6 #

b) wKa2<-->bKa4  

  1.e2-e1=R a7-a8=Q   2.Re1-a1 Qa8-g2 #

The Dalton theme
Pinning and unpinning are favorite thematic components with composers. One of the more appealing patterns has an unpinned piece pinning the piece that just unpinned it. The pinning is often by discovery and is sometimes a self-pin by the unpinning piece, the unpinning and pinning taking place with a single move.
The thematic moves are not necessarily consecutive. In a helpmate, for example, black will often happily step right into the pin with the king after the unpinned piece has prepared the pin. The following query will pick up all of the aforementioned patterns and more.

cql(quiet)
initial

function hasPattern() {
  line
    --> .*
    --> {
        piece Unpinner = move from pin from [Aa]
        piece Unpinned = pin through [Aa]
        }
    --> (.*
      --> move from Unpinned
      --> .*){0 1}
    --> pin from Unpinned through Unpinner
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not hasPattern() then SeriesAbort = 1
  false
} else {
  if not hasPattern() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The line filter will actually match multiple unpinning-pinning instances in the same solution, and many of the matching compositions have multiple pieces engaged either separately or in a cascading series of such acts. Some of the compositions are just downright obscene.
Edit the line group repetition factor to read {0 0} to match only the compositions in which the unpinning piece steps right into a self-pin in the same move. Changing the repetition factor to {1 1} will filter for the complement of that result.

The Dalton is fairly commonplace both inside and outside of the twinning domain. The helpmate by Csák is a pinning/unpinning extravaganza which just happens to include that pattern.

[Event "1st-2nd Prize, Pat a Mat"]
[Site "Yet Another CPDB"]
[Date "2018.06.??"]
[Round "12754100"]
[White "Csák, János"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Add black Bd5"]
[FEN "8/4p3/KR1rPb2/1B1rp3/p1q1P2p/3P3k/4R3/8 b - - 0 1"]


a) 

  1.Rd5*d3 Rb6*d6   2.Qc4*e6 Bb5-d7   3.Qe6-g4 Rd6*d3 #

b) bBd5  

  1.Bd5*e6 Bb5*c4   2.Rd6*d3 Rb6-b3   3.Rd3-g3 Bc4*e6 #

The pendulum
The definition of this theme (maneuver) is devilishly difficult to tie down. The most common is characterized as the forced repetition of moves between two squares. But it may also be between more than two squares, or across a wide swing of squares where repetition is not the main issue. For any of the definitions along that spectrum, the pattern is not of much interest in a twinning context.
But we have discovered a pendulum-like pattern expressed across a series of twins in which some number of the defined points of the pendula (the pivot, the equilibrium position, and the two oscillation extremities) intersect across solutions. The intersecting points do not necessarilly correlate (e.g., a pivot point for one may be an oscillation extremity for the other).

A piece — the same piece across the series — visits every one of the points of a pendulum over the length of each solution. Our guess is that only a queen would have the maneuverability to pull this off. The three points in the swing lie in a line (orthogonal or diagonal), as do the equilibrium and the pivot. The rest point is not necessarily at or even near the midpoint of the swing, though the visual effect is more appealing the closer it is.

Any given solution may have more than one pendulum (and some do). Any given series may have pendula transcribed by opposing sides (and some do). Loosening the constraints given in the query below will match some of those compositions, but then the results look less and less as if the pattern is intentional.

cql(quiet)
initial

function Pendulum() {
  flipcolor {
    penMoves = Q
    line --> .* --> penMoves = penMoves | move to . from Q
    Swing = ray(penMoves penMoves penMoves)
    Equil = penMoves & between(Swing Swing)
    Pivot = penMoves & ~(Swing | Equil)
    if Q == 1 and anydirection 2 7 Pivot & Equil == 1
      then {
        //message(Swing " " Equil " " Pivot)
        penMoves
      } else ~.
  }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $Pendulum = Pendulum()
  false
} else {
  if (sort "Common Points" $Pendulum & Pendulum()) < 1
    then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The bulk of the work for this query is assigned to the Pendulum() function. After accumulating the squares visited by the thematic piece, the four points of interest are acquired. Note that the endpoints of the swing are only used in determining the rest point(s) and pivot(s). A pivot may lie on any line relative to a rest point, but the line of the swing is obviously already excluded as we've established that the pivot is not in that line. The range (2 7) puts a bit of distance between the pivot and the rest point.
We allow for as little as a single intersecting point between solutions, but it seems to us that the greater the number of points the stronger the pattern. And so we sort the results by the number of points shared so as to move the strongest matching series to the top.

The astute observer might have noticed that we only look for the pattern in the mainline. We might get a larger sample of matching series if we also looked in all variations of actual play, but we'll leave that as an exercise for the time being.

We do find the pattern in the mainline of the composition by Larin, a direct mate with some interesting byplay. For the base position depicted in the diagram, we've highlighted the visited points of the respective pendula, with intersecting points in red.

[Event "1st Comm., Чорно-білі стежини"]
[Site "Yet Another CPDB"]
[Date "2009.??.??"]
[Round "12116300"]
[White "Larin, Rudolf Michailowitsch"]
[Black "#3 -- Twins -- Actual+Virtual+Set Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Block:Block-Pendulum"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#3"]
[TwinB "Move f2 h4"]
[FEN "8/8/1p6/bP6/8/p7/P3pQ2/1K1kB3 w - - 0 1"]


a) 

   1.Qf2-h4 ! zugzwang.
      1...Ba5*e1
          2.Qh4-a4 +
              2...Kd1-d2
                  3.Qa4-d4 #
      1...Ba5-d2
          2.Qh4-d4 threat:
                  3.Qd4*d2 #
              2...Kd1*e1
                  3.Qd4-g1 #
      1...Ba5-c3
          2.Be1*c3 threat:
                  3.Qh4-e1 #
                  3.Qh4-d8 #
                  3.Qh4-a4 #
                  3.Qh4-d4 #
              2...e2-e1=Q
                  3.Qh4*e1 #
              2...e2-e1=S
                  3.Qh4*e1 #
              2...e2-e1=R
                  3.Qh4*e1 #
              2...e2-e1=B
                  3.Qh4*e1 #
                  3.Qh4-g4 #
                  3.Qh4-h5 #
      1...Ba5-b4
          2.Be1*b4 threat:
                  3.Qh4-e1 #
                  3.Qh4-d8 #
                  3.Qh4-d4 #
              2...e2-e1=Q
                  3.Qh4*e1 #
              2...e2-e1=S
                  3.Qh4*e1 #
              2...e2-e1=R
                  3.Qh4*e1 #
              2...e2-e1=B
                  3.Qh4*e1 #
                  3.Qh4-g4 #
                  3.Qh4-h5 #


b) wQf2-->h4  

   1.Qh4-f2 ! zugzwang.
      1...Ba5*e1
          2.Qf2-g1 zugzwang.
              2...Kd1-d2
                  3.Qg1-d4 #
      1...Ba5-d2
          2.Qf2-d4 threat:
                  3.Qd4*d2 #
              2...Kd1*e1
                  3.Qd4-g1 #
      1...Ba5-c3
          2.Be1*c3 threat:
                  3.Qf2-e1 #
                  3.Qf2-d4 #
              2...e2-e1=Q
                  3.Qf2*e1 #
                  3.Qf2-c2 #
              2...e2-e1=S
                  3.Qf2*e1 #
                  3.Qf2-d2 #
              2...e2-e1=R
                  3.Qf2*e1 #
                  3.Qf2-c2 #
                  3.Qf2-d2 #
              2...e2-e1=B
                  3.Qf2*e1 #
                  3.Qf2-c2 #
                  3.Qf2-f3 #
      1...Ba5-b4
          2.Be1*b4 threat:
                  3.Qf2-e1 #
                  3.Qf2-d4 #
              2...e2-e1=Q
                  3.Qf2*e1 #
                  3.Qf2-c2 #
              2...e2-e1=S
                  3.Qf2*e1 #
                  3.Qf2-d2 #
              2...e2-e1=R
                  3.Qf2*e1 #
                  3.Qf2-c2 #
                  3.Qf2-d2 #
              2...e2-e1=B
                  3.Qf2*e1 #
                  3.Qf2-c2 #
                  3.Qf2-f3 #

The leapfrog
Two pieces alternate in leaping over each other across starting positions in the series, tracing a geometric pattern as they go. One of the pieces jumps from edge to edge, while the other jumps from corner to corner. The leapers represent the only changes to the board.
The starting position for each twin in the series is a continuation from the last. The geometric pattern traced is typically a square, but may as easily be a triangle or even a straight line (in which case, of course, there are no corners involved unless we find ourselves in a topologically very strange universe). The query is deceptively simple.

cql(include libcql/libhlp.cql quiet)
initial

function xSq(y x) { if XOR(x y) == 2 then XOR(x y) & x else ~. }

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent LeapCount = 0
  persistent $pBoard = [Aa]
  persistent $ePiece = []
  false
} else {
  if TwinCount % 2 == 1
    then $ePiece = xSq($pBoard [Aa])
    else LeapCount += 
           #($ePiece & between(xSq($pBoard [Aa]) xSq([Aa] $pBoard)))
  $pBoard = [Aa]
  TwinCount -= 1
  if TwinCount == 0 and LeapCount == 3
    then true
    else false
}

The modulus operator gives us the alternation we need as the pieces leap over each other. The apparent convention is that the edge piece jumps first (we have no idea why that would be), and so we go with that assumption.
The xSq() function requires a bit of an explanation. The XOR operation between two positions (bitboards representing occupied squares) gives us changes to the board, but tells us nothing about from-ness or to-ness. For that, we must take the intersection of the result of the XOR operation with the bitboard from which or to which the transition is taking place. For example, if we want to know the square to which a leaping piece leaps, we should take the intersection of the set of board changes with the bitboard representing the current position (squares occupied).

Once we have the square on which the edge piece has landed, we know that it must lie between the squares from which and to which the corner piece leaps. The cycle repeats three times when tracing a square figure.

The query matches a couple of prize-winning compositions, of which we give a direct mate below. As appealing as the leapfrog patterns are, the mating patterns across solutions for both compositions are equally impressive. It should not surprise us that this pattern is rare.

[Event "1st Prize, Соціалістична Харківщина"]
[Site "Yet Another CPDB"]
[Date "1963.??.??"]
[Round "10121600"]
[White "Тогер, Александр Вульфович"]
[Black "#3 -- Twins -- Actual+Virtual Play"]
[Result "1-0"]
[BlackElo "7"]
[Keywords "Echo mates:Task"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#3"]
[TwinB "Move d2 e3"]
[TwinC "Continued Move e2 e4"]
[TwinD "Continued Move e3 d4"]
[TwinE "Continued Move e4 c4"]
[TwinF "Continued Move d4 c3"]
[TwinG "Continued Move c4 c2"]
[TwinH "Continued Move c3 d2"]
[FEN "1K6/2p5/2P5/8/7P/N2k2N1/3BR3/8 w - - 0 1"]


a) 

   1.Re2-f2 ! zugzwang.
      1...Kd3-d4
          2.Rf2-f5 zugzwang.
              2...Kd4-d3
                  3.Rf5-d5 #


b) wBd2-->e3  

   1.Re2-e1 ! zugzwang.
      1...Kd3-c3
          2.Re1-b1 zugzwang.
              2...Kc3-d3
                  3.Rb1-b3 #


+c) wRe2-->e4  

   1.Re4-e5 ! zugzwang.
      1...Kd3-c3
          2.Re5-b5 zugzwang.
              2...Kc3-d3
                  3.Rb5-b3 #


+d) wBe3-->d4  

   1.Re4-f4 ! zugzwang.
      1...Kd3-d2
          2.Rf4-f1 zugzwang.
              2...Kd2-d3
                  3.Rf1-d1 #


+e) wRe4-->c4  

   1.Rc4-b4 ! zugzwang.
      1...Kd3-d2
          2.Rb4-b1 zugzwang.
              2...Kd2-d3
                  3.Rb1-d1 #


+f) wBd4-->c3  

   1.Rc4-c5 ! zugzwang.
      1...Kd3-e3
          2.Rc5-f5 zugzwang.
              2...Ke3-d3
                  3.Rf5-f3 #


+g) wRc4-->c2  

   1.Rc2-c1 ! zugzwang.
      1...Kd3-e3
          2.Rc1-f1 zugzwang.
              2...Ke3-d3
                  3.Rf1-f3 #


+h) wBc3-->d2  

   1.Rc2-b2 ! zugzwang.
      1...Kd3-d4
          2.Rb2-b5 zugzwang.
              2...Kd4-d3
                  3.Rb5-d5 #

Threat reversal
The key and accompanying threat are reversed across solutions. The pattern is expressed entirely in the mainline, with an intervening null move. We do not restrict consideration to the obvious 2-series, as the pattern is sometimes larger than a single reversal (see the matching series below).

cql(quiet variations)
initial

function ThreatLine(key threat) {
  line
    --> move primary
    --> hascomment "threat" and
          key = move from . previous | move to . previous
    --> move null previous and not child(1) and
          threat = move from . | move to .
  key != threat  // catch double-back threats
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAffirm = 0
  persistent $Key = ~.
  persistent $Threat = ~.
  ThreatLine($Key $Threat)
  false
} else {
  Key = ~.  Threat = ~.
  if ThreatLine(Key Threat) and
      Key == $Threat and Threat == $Key
    then SeriesAffirm = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAffirm == 1
    then true
    else false
}

The ThreatLine() function returns from/to square sets for each of the moves under consideration. The child filter eliminates from consideration threat lines having dual threats. We also check that the threat is not simply a double-back of the key, which would be rather difficult to reverse.
The pattern we're looking for is simple: each of the square sets of the threat line matches its counterpart across some twin in the series. Per the usual, there's no reason to bother with piece types.

The matching composition by Lysjonok delivers a pair of threat reversals across a 4-series. The query requires only a single reversal but we've never been averse to serendipitous discovery. The patterns across solutions leave us with an lasting impression.

[Event "3rd Prize, Сельское хозяйство Белоруссии"]
[Site "Yet Another CPDB"]
[Date "1990.03.??"]
[Round "10892400"]
[White "Lysjonok, Nikolai Nikolajewitsch"]
[Black "#3 -- Twins -- Actual+Virtual Play"]
[Result "1-0"]
[BlackElo "3"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#3"]
[TwinB "move a4 a5"]
[TwinC "move f4 e5"]
[TwinD "move f4 e3"]
[FEN "8/8/2N5/8/p4p2/2B5/7R/2k4K w - - 0 1"]


a) 

   1.Rh2-a2 ! threat:
          2.Sc6-d4 threat:
                  3.Ra2-a1 #
      1...Kc1-b1
          2.Sc6-b4 threat:
                  3.Ra2-a1 #


b) bPa4-->a5  

   1.Sc6-d4 ! threat:
          2.Rh2-a2 threat:
                  3.Ra2-a1 #
      1...Kc1-b1
          2.Sd4-b3 threat:
                  3.Rh2-b2 #


c) bPf4-->e5  

   1.Sc6-b4 ! threat:
          2.Rh2-e2 threat:
                  3.Re2-e1 #
      1...Kc1-d1
          2.Sb4-d3 threat:
                  3.Rh2-d2 #


d) bPf4-->e3  

   1.Rh2-e2 ! threat:
          2.Sc6-b4 threat:
                  3.Re2-e1 #
      1...Kc1-d1
          2.Sc6-d4 threat:
                  3.Re2-e1 #

Four corners
A piece starting out on one corner of the board in the base position moves to occupy every other corner of the board in the starting positions across the series. The starting positions are otherwise constant.
We'll accumulate the corners visited by the piece in a persistent set variable, finally testing that every corner was checked off over the course of the series. Note that we only track piece type and color rather than the actual piece, but taken with the complement of constraints that is good enough.

cql(include libcql/libhlp.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent CT = 0
  persistent $Occupied = [Aa]
  persistent $Corners = onCorners()
  if $Corners == 1
    then CT = colortype $Corners
    else CT = 0
  false
} else {
  OnC = onCorners()
  if OnC == 1 and CT == colortype OnC and XOR($Occupied [Aa]) == 2
    then $Corners = $Corners | OnC
  TwinCount -= 1
  if TwinCount == 0 and CT != 0 and $Corners == 4
    then true
    else false
}

The condition XOR($Occupied [Aa]) == 2 tells us that two squares have changed (in terms of occupation) between starting positions, presumably the corner from which the piece has moved and the corner to which the piece has moved. Nowhere do we stipulate that pieces are constant across positions, only that squares occupied are constant. But the pattern as stipulated is dominant enough to prevail.
The query matches the following composition, with the white queen moving to occupy every corner of the board across the twin series. Note that as the white queen establishes her pattern across the board, the black king steps through his own cross pattern across solutions.

[Event "1st Prize, TT 157 Superproblem"]
[Site "Yet Another CPDB"]
[Date "2015.12.13"]
[Round "12623200"]
[White "Argirakopoulos, Themis & Prentos, Kostas"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "3"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Move a1 a8"]
[TwinC "Move a1 h8"]
[TwinD "Move a1 h1"]
[FEN "6K1/6b1/1np1rp2/1b1k4/p1p1q3/2r1pp2/1p1P3p/Q1n5 b - - 0 1"]


a) 

  1.Kd5-c5 d2*c3   2.Qe4-d5 Qa1-a3 #

b) wQa1-->a8  

  1.Kd5-d6 d2-d4   2.Sb6-d5 Qa8-d8 #

c) wQa1-->h8  

  1.Kd5-e5 d2*e3   2.Ke5-f5 Qh8-h5 #

d) wQa1-->h1  

  1.Kd5-d4 d2-d3   2.Kd4*d3 Qh1-d1 #

The Klasinc theme
We have two thematic pieces (friendlies). Over the course of the solution, the one piece conducts a switchback, while the other piece crosses over the vacated square before the switch is complete. The thematic moves are not necessarily consecutive.

The second piece's maneuver might include a stopover on the vacated square before moving on to make way for the switch. If there is no stopover, the crossing piece is necessarily a line piece. With a stopover, not so much. A single query handles both cases of the pattern.

cql(quiet)
initial  btm

function hasPattern() {
  sort "Line length"
    line singlecolor
      --> .*
      --> { piece P1 = move from .  Critical = P1 }
      --> .*
      --> Critical & between(move from .  move to .)
            or {move to Critical from ~P1  comment("Stopover")}
      --> .*
      --> move from P1 to Critical
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not hasPattern() then SeriesAbort = 1
  false
} else {
  if not hasPattern() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Sorting by the length of the line, the stopover patterns will naturally move their way to the top of the matching series. Note that the move of the crossing piece off of the critical square — making way for the switchback — need not be stipulated explicitly, for without it the switching piece could not complete its maneuver.
While the pattern is intra-solution, in a twinning context there may be — and usually are — other thematic components that express across the series. The helpmate by Agapow and Nefjodow expresses the theme for every solution of a 3-series, with different thematic pieces for each solution but with the same mating piece.

[Event "1st Prize, Уральский проблемист"]
[Site "Yet Another CPDB"]
[Date "1997.??.??"]
[Round "11234700"]
[White "Agapow, Igor Alexejewitsch & Nefjodow, Wladislaw Walerjewitsch"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "2"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move f2 f4"]
[TwinC "Move h8 b8"]
[FEN "7B/4p3/K5p1/2NPP1p1/3P3r/3nkn2/3ppb2/1q5b b - - 0 1"]


a) 

  1.Sf3*e5 Sc5-e6   2.Bh1-e4 Se6-f4   3.Se5-f3 Sf4-g2 #

b) bBf2-->f4  

  1.Bf4*e5 Sc5-d7   2.Rh4-e4 Sd7-f6   3.Be5-f4 Sf6-g4 #

c) wBh8-->b8  

  1.Sd3*e5 Sc5-b3   2.Qb1-e4 Sb3-a1   3.Se5-d3 Sa1-c2 #

Organ Pipes
Sam Loyd made many contributions to the art form, but the Organ Pipes theme may well be his most notable: two adjacent rooks flanked by bishops, all aligned along an orthogonal line, setting the stage for a doubled-up Grimshaw (a challenging theme by any measure). The thematic pieces are usually black and the solution is usually a two-mover, but there are exceptions.
In a twinning context, the organ pipe pattern on the board holds across twins but the full pattern of self-interferences is expressed across solutions. We'll test for the presence of both aspects of the pattern, but we look to a specific move pattern as being strongly suggestive that the interference is present. After all, it is nearly sufficient to infer that the interference is present because the organ pipe board pattern is so uncommon.

cql(quiet)
initial  btm

function hasPipes($B $R) {
  ray orthogonal ($B $R $R $B) and between($B $B) == 2
}

function hasIF($B $R) {
  ifMoves = ~.
  line --> .* --> ifMoves = ifMoves | move from ($B|$R) to orthogonal 1 $R
  ifMoves == 2
}

function hasPattern() { flipcolor {hasPipes(B R) and hasIF(B R)} }

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not hasPattern() then SeriesAbort = 1
  false
} else {
  if not hasPattern() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The hasPipes() function verifies that the board pattern is present, with the organ pipes arranged along an orthogonal line and with no space between the pieces. The hasIF() function determines that exactly two of the thematic pieces move to their respective interfering posts in the course of a solution. If both patterns are present and accounted for across the series, the larger pattern is confirmed for one or the other of the sides.
The composition by Van Gool demonstrates that rare case in which the thematic pieces are white and the solutions are three-movers. The twin specification addresses the alternating pinning of the white rooks against their king, allowing for the theme to play out.

[Event "Probleemblad"]
[Site "Yet Another CPDB"]
[Date "1995.07.??"]
[Round "11130700"]
[White "Van Gool, Johann Christoffel"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Organ pipes"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move e8 d8"]
[FEN "4K3/2BRRBp1/n1b2bP1/2n5/2PppP2/4p3/4k3/8 b - - 0 1"]


a) 

  1.Ke2-d3 Re7-e6   2.Kd3*c4 Bc7-d6   3.Kc4-d5 Re6-e5 #

b) wKe8-->d8  

  1.Ke2-f3 Rd7-d6   2.Kf3*f4 Bf7-e6   3.Kf4-e5 Rd6-d5 #

The Baltic theme
One will typically see this theme expressed in a single helpmate having multiple solutions, where black plays on the same square at the same ply across solutions (possibly at multiple ply) and white mates on the same square across solutions. The respective moves are made by different pieces for a given side.
In a twinning context, black opens thematically across the series and white mates thematically across the series. The black thematic play is limited to the first ply of each solution.

The plan for the query is simple. Qualifying twins will satisfy a set of criteria relative to the base solution. We first pick up the opening move by black (from and to squares) from the base position. Likewise for the mating move. Then for each twin the opening move by black must match the base destination square and must not match the base source square. Ditto for the mating move. Source squares for both moves must be unique across the series.

cql(quiet)
initial  btm

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $fromOpen = move from .
  persistent $toOpen = move to .
  find {
    terminal
    persistent $fromMate = move from . previous
    persistent $toMate = move to . previous
  }
  //if move from k then SeriesAbort = 1
  false
} else {
  if move from . in $fromOpen  or $toOpen != move to .
      or find {
        terminal
        move from . previous in $fromMate or
          $toMate != move to . previous
        $fromMate = $fromMate | move from . previous
      }
    then SeriesAbort = 1
  $fromOpen = $fromOpen | move from .
  //if move from k then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

It's not clear that the black king should be a thematic candidate, but we allow for that possibility as there are numerous matching compositions in which the king plays a role. Note that we maintain a record of all source squares as we move across twins, so that we can be sure that all thematic moves are by different pieces across the series.
The theme is rather popular with the twinning crowd, with most compositions in the 2-series class. The helpmate by Zidek expresses the theme across a 3-series, with thematic pieces matching in type for each solution.

[Event "3rd Place, 4th WCCT E"]
[Site "Yet Another CPDB"]
[Date "1989.??.??"]
[Round "10844400"]
[White "Zidek, Alexander"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "2"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move e3 f2"]
[TwinC "Move e3 a5"]
[FEN "4B3/rN2pb2/1p5p/3kn3/p2n4/2p1P3/3r3q/K7 b - - 0 1"]


a) 

  1.e7-e6 Be8-b5   2.Bf7-e8 Bb5-d3   3.Be8-c6 e3-e4 #

b) wPe3-->f2  

  1.Bf7-e6 f2-f3   2.Qh2-e2 Be8-g6   3.Qe2-c4 Bg6-e4 #

c) wPe3-->a5  

  1.Sd4-e6 Sb7-c5   2.Kd5-d6 a5*b6   3.Rd2-d5 Sc5-e4 #

The monkey theme
We have no idea why the world's problemists would be dissing our intellectual and cultural superiors, but there are a couple of flavors of this theme that are of interest to us despite the name. The classic theme has the moves between opposing pieces shadowing or reflecting one another in a pattern of geometric equivalence across the solution. Generally, the pieces involved in any given pairing of moves are of the same piece type, and often the pattern involves the same two thematic pieces across the entire length of the solution.
In a twinning context the classic pattern will express across the first two ply of each twin in the series, and (for whatever reason) is then referred to as a magnet rather than a monkey. If the magnet assumes a cyclic pattern, then apparently we're back to being a monkey. (One could not make this stuff up.)

We'll first address the pattern which expresses across the length of the solution for each twin in the series. The thematic pieces at any given pairing will be of the same type, but may vary in type across the solution. Every solution of the series must express the pattern.

cql(quiet)
initial

function hasShadow() {
  sort "Iterations" {
    line
      --> (  // paired positions (moves)
            piece P1 = move from .
        --> {  // the second position (move) of the pair
              piece P2 = move from .
              type P1 == type P2
              parent:{rank P1} - rank P1 == rank P2 - child:{rank P2}
                  and
              parent:{file P1} - file P1 == file P2 - child:{file P2}
            }
          ) {2 100}
    / 2 }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not hasShadow() then SeriesAbort = 1
  false
} else {
  if not hasShadow() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

For the coordinate system mapped by the file and rank filters, and for two pieces [P1 P2] moving across the board, let us define geometric equivalence in their movements from square to square as:
- deltaX P1 == deltaX P2 and deltaY P1 == deltaY P2
where sign is significant and [X,Y] are the mappings by the two filters. The hasShadow() function tests for that equivalence over some length of a solution established by the repetition factor applied to the line group.

Note that we do not check that the pattern holds across the entire solution. We have caught sight of the occasional composition with thematic intermezzo, or even a slight disqualifying twist on the theme which is interesting in its own right.
The helpmate by Scharkow expresses the pattern over three moves and by two piece types. The same thematic pieces are involved in both solutions.

[Event "Special Prize, 10-й МК З.Бирнов"]
[Site "Yet Another CPDB"]
[Date "1990.??.??"]
[Round "10885900"]
[White "Scharkow, Nikolai Abramowitsch"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Model mates:Monkey theme:Unpinning"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move a2 h4"]
[FEN "4K2n/8/3p4/3nN1p1/5pp1/p1Bbrpqp/k1p1r3/2b5 b - - 0 1"]


a) 

  1.Bd3-e4 Bc3-d4   2.Sd5-c3 Se5-d3   3.Sc3-b1 Sd3*c1 #

b) bKa2-->h4  

  1.Sd5-e7 Se5-f7   2.Bd3-g6 Bc3-f6   3.Bg6-h5 Bf6*g5 #

The cyclic pattern is a bit more difficult to construct as it expresses across multiple solutions. The short explanation for our approach to the query is: collect the moves across the series and then see if the pattern for each thematic pairing can be found among the moves played as some set of the recorded source and destination squares.
It's easier to achieve than it is to explain, so let's just go right to the source.

cql(quiet)
initial  btm

function hasShadow() {
  line
    --> piece P1 = move from .
    --> {
        piece P2 = move from .
        parent:{rank P1} - rank P1 == rank P2 - child:{rank P2}
        parent:{file P1} - file P1 == file P2 - child:{file P2}
        }
}

function vSquares(fodd todd feven teven) {
  type move from . == child:{type move from .}
  line
    --> {fodd = fodd | move from .  todd = todd | move to .}
    --> {feven = feven | move from .  teven = teven | move to .}
}

function isCyclic(fodd todd feven teven) {
  square all O1 in todd
    square O2 in fodd
      square E1 in teven
        square E2 in feven {
          rank O1 - rank O2 == rank E1 - rank E2
          file O1 - file O2 == file E1 - file E2
          //message(O1 O2 E1 E2)
        }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $fromOdd = ~.
  persistent $toOdd = ~.
  persistent $fromEven = ~.
  persistent $toEven = ~.
  if TwinCount < 2 then SeriesAbort = 1
  if hasShadow() or not vSquares($fromOdd $toOdd $fromEven $toEven)
    then SeriesAbort = 1
  false
} else {
  if hasShadow() or not vSquares($fromOdd $toOdd $fromEven $toEven)
    then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and isCyclic($fromOdd $toOdd $fromEven $toEven)
    then {
      //message($fromOdd $toOdd $fromEven $toEven)
      true
    } else false
}

First of note is that we insist that the thematic pieces are all of the same type, else the query becomes overly busy with bitboards. We insist on this rather awkwardly, relying on the diminishing odds that they are not all of the same type when the test is applied across the series. Secondly, we only consider cycles expressed across a 3-series (or greater), as anything less than that is not much of a cycle.
The hasShadow() function should be familiar from the previous query, though our purpose here is to ensure that no one solution actually has one piece shadowing the other. The vSquares() function gathers the moves (from and to squares) into their respective sets for later processing.

And finally we come to the hand-waving magic of the isCyclic() function. We have the sets of squares from which and to which the [presumably] thematic pieces have moved. If, for every square to which one of those pieces has moved, there is some set of squares for which the shadowing pattern holds, we're guessing we have the realization of the cycle.

The cyclic pattern for this theme is a rarity, and has but three matching compositions anywhere in the galaxy that we can find (the third by Bogdanow has been added to the twins database with origin credited to Chess Leopolis Magazine). The helpmate given below (also by Bogdanow) demonstrates a cycle by two bishops across a 3-series.

[Event "2nd Honorable Mention, Chess Leopolis"]
[Site "Yet Another CPDB"]
[Date "2007.??.??"]
[Round "11974800"]
[White "Bogdanow, Jewgenij Michajlowytsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "2"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "move b4 f8"]
[TwinC "move b4 f2"]
[FEN "4r3/4n3/6P1/np1P4/1kbB4/2pPpp2/2P3q1/3K2b1 b - - 0 1"]


a) 

  1.Bc4-b3 Bd4-e5   2.Bb3-a4 Be5-d6 #

b) bKb4-->f8  

  1.Bc4*d5 Bd4*e3   2.Bd5-g8 Be3-h6 #

c) bKb4-->f2  

  1.Bc4*d3 Bd4*c3   2.Bd3-f1 Bc3-e1 #

Board transforms

The Popeye solving engine allows for shifts, flips and rotates in its twin specifications and we find a fair number of series employing these transforms in the twins database. Though the transforms are not necessarily thematic, themselves, they are a means to an end and often lend an interesting effect to the composition. Most of the examples that follow will look for some incidental thematic component which may be a consequence of the transformed board.

When looking for transformed boards across a series, we'll borrow from the Transforming Boards companion document for an interface to our transform mechanics. For a couple of examples, we'll also demonstrate the use of regular expressions applied to the twin specifications in the PGN header as an alternative approach to the query, most often employed in special cases.

Shifting
The shift is probably the most commonly applied transform found in a twinning specification. We'll begin with a simple query looking for a series having some minimum number of twins in which every twin is shifted and the stipulation is unchanged.

cql(include libcql/libxfm.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Occupied = [Aa]
  persistent Stip = tag "Stipulation"
  if TwinCount < 2 then SeriesAbort = 1
  false
} else {
  if not isShift(Occupied [Aa]) or Stip != tag "Stipulation"
    then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Normally, shifting pieces off the board is frowned upon. It's rare, but it does happen. Intentionally. And it does occasionally earn honors from the committee.
We'll search for those series in which each twin shifts pieces off. Note that the order in which the boards are given in the isShift() argument list allows us to match shifted boards that have fallen off the edge.

cql(include libcql/libxfm.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Occupied = [Aa]
  false
} else {
  if not (isShift([Aa] Occupied) and #Occupied != #[Aa])
    then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Flipping
Transforming a position into or out of castling availability seems to be a favorite with the twinning crowd. With the following query we'll look for flipped boards across the series in which one side or the other (or both) either flips into or flips out of a castling option.

cql(include libcql/libxfm.cql quiet)
initial

// Return the castling availability field.
// (The expression is borrowed from the online CQL reference.)
function CAF() {
  fen ~~ "^([^ ]+) ([bw]) ([KQkq]+|-) ([a-h][1-8]|-) (\d+) (\d+)"
  \3
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 1
  persistent Occupied = [Aa]
  persistent Castling = CAF()
  false
} else {
  if isFlip(Occupied [Aa])
    while ("KkQq" ~~ ".")
      if (\0 in Castling and not \0 in CAF()) or
         (not \0 in Castling and \0 in CAF())
        then SeriesAbort = 0
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Because the query tests for the transform based solely on occupied squares, we do pick up a couple of false positives on the flipping front. For a technique one might use in correcting that deficiency, see the example below under the Transforms++ heading.
Next we'll look for flips about a diagonal in which one or both of the kings is sitting on the diagonal and is therefore unmoved.

cql(include libcql/libxfm.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 1
  persistent Occupied = [Aa]
  false
} else {
  if  Occupied == Flip([Aa] a1 h8) and [Kk] & diagonal a8
         or
      Occupied == Flip([Aa] a8 h1) and [Kk] & diagonal h8
    then SeriesAbort = 0
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Rotating
We'll look for compositions in which one or more pawns either rotates into or out of a promotable configuration in every twin of the series. We also stipulate that promotion actually plays a role in some phase of one or more of the twins, even if only as a threat.

cql(include libcql/libhlp.cql include libcql/libxfm.cql quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Found = 0
  persistent Occupied = [Aa]
  persistent Promotable = Pa-h7 | pa-h2
  if find move promote A then Found = 1
  false
} else {
  if not (isRotate(Occupied [Aa]) and XOR(Promotable  Pa-h7 | pa-h2))
    then SeriesAbort = 1
  if find move promote A then Found = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and Found == 1
    then true
    else false
}

Rotating through all four orientations is a popular element of many twinning themes. We'll search for those quad series in which the theme expressed across the series qualifies — at least in part — as an Allumwandlung.

// Rotating Allumwandlung.  (CQLv6.2)
cql(include libcql/libxfm.cql quiet)
initial

dictionary promoPT
function promoLog() {
  find {
    promoSq =? move to . promote A previous
    promoPT[colortype promoSq] = ""
  }
}

if player black "Twins"
then {
  unbind promoPT
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Occupied = [Aa]
  promoLog()
  false
} else {
  if isRotate(Occupied [Aa]) then promoLog()
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0 and #promoPT == 4
    then true
    else false
}

We're a little bit lazy in that we don't bother to check that all four promotions are by the same side or that there might be more than one promotion in a solution or that the promotions all occurred in actual play. But, seriously, what are the odds? The query turns out to be quite accurate in its results, and the rare exception tends to be an interesting composition in any event.

Stringin' it
For most users and for most queries, the transform library is probably the easier way to go. For those familiar with the use of regular expressions — and especially in certain exceptional cases — we'll demonstrate an alternative technique which may be more appropriate to the task at hand.
Occasionally, we'll see a twin specification that applies multiple transforms to the board. If we were to search for these compound transforms employing the library interfaces, we would likely have time for a long sleep while waiting for the results. Instead, we'll search the PGN tags carrying each twin's specification for any string having multiple transform specs.

Of particular note are the flip'n'shift and shift'n'flip specifications. Combinations of shifts and flips effectively allow us to flip about an arbitrary line (shifting the bisector as it were) or to flip about a rank or file. Compound transforms might help us later on to look for certain symmetries.

cql(quiet)
initial

function tagSwitch(suffix) {
       if suffix == "B" then TagVal = tag "TwinB"
  else if suffix == "C" then TagVal = tag "TwinC"
  else if suffix == "D" then TagVal = tag "TwinD"
  else if suffix == "E" then TagVal = tag "TwinE"
  else if suffix == "F" then TagVal = tag "TwinF"
  else if suffix == "G" then TagVal = tag "TwinG"
  else TagVal = ""
  TagVal
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent BaseCount = TwinCount
  persistent SeriesAbort = 1
  false
} else {
  TwinSpec = tagSwitch(ascii 65 + BaseCount - TwinCount + 1)
  if TwinSpec ~~ "([Mm]irror.+|[Ss]hift.+){2,}" then SeriesAbort = 0
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

With the tagSwitch() function we kludge our way around a minor CQL inconvenience. The tag filter will accept only a string literal as argument, and so we switch our way through the twin tag suffixes with a bit of a sledge hammer.
Though we could just iterate our way through all of the specifications from the base position, we might actually want to do something useful with the corresponding twin and so we match the actual transformed twin. Note that this query obviously doesn't work with the zeroposition series.

By the way, for a very cool compound rotate'n'shift 4-series, see Rosner (2013 - Pat a Mat).

Most shifts are applied in the horizontal or vertical by one or two squares. It's natural to wonder what's going on with the exceptions. The following query borrows an idea from the online reference to find twins that have been shifted in a direction having some slope (other than infinite) or in the horizontal or vertical by an exceptional extent.

cql(quiet)
initial

function tagSwitch(suffix) {
       if suffix == "B" then TagVal = tag "TwinB"
  else if suffix == "C" then TagVal = tag "TwinC"
  else if suffix == "D" then TagVal = tag "TwinD"
  else if suffix == "E" then TagVal = tag "TwinE"
  else if suffix == "F" then TagVal = tag "TwinF"
  else if suffix == "G" then TagVal = tag "TwinG"
  else TagVal = ""
  TagVal
}

Scale = 100
function dSquares(x y) {
  SqX = makesquare x  SqY = makesquare y
  deltaRank = Scale * (rank SqX - rank SqY)
  deltaFile = Scale * (file SqX - file SqY)
  sqrt(deltaRank*deltaRank + deltaFile*deltaFile)
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent BaseCount = TwinCount
  persistent SeriesAbort = 1
  false
} else {
  TwinSpec = tagSwitch(ascii 65 + BaseCount - TwinCount + 1)
  if TwinSpec ~~ "[Ss]hift\s+([a-h][1-8])\s+([a-h][1-8])"
    then {
      Distance = dSquares(\1 \2)
      if Distance >= 4*Scale or Distance % Scale != 0
        then {
          SeriesAbort = 0
          message(\1 " " \2 " " Distance)
        }
    }
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Transforms++
Typically, the transform stands alone as a twin specification. But it may also be joined by other board mods either within a single spec or as a continuation. Pieces may be added or removed or moved or exchanged pre- or post-transform.
So what we're looking for is effectively a near miss where most of the pieces on the board are transformed, but with an exception or two. We'll search for near shifts, since those are the most common and since they come in a variety of flavors. Among the matching series, for example, one will find edge-to-edge rotations where pieces shifted off one edge of the board are shifted back onto the opposite edge.

Not all of the qualifying series are even achieved with a shift, which rules out grepping through the twin specifications in the PGN header. Some "shifts" are realized as a collection of moves, and some near symmetric positions may be flipped and appear to be shifted. And as mentioned above, the transform may be applied as a continuation to a prior specification.

Most of the examples in this section get by with transforming occupied squares without regard for piece type or color. The odds have been in our favor up to this point. That rolling of the dice will not get the job done when we're looking for a near miss on a shift.

Ideally, we would consider the board piece by piece in determining whether most of it has been consistently shifted, but the query is already overly compute-intensive. Instead, we'll poll the board by piece colortype, deciding that we have a near miss if some arbitrarily chosen majority of the piece types have identical shift signatures. Not perfect, but good enough.

// Transform near miss.  (CQLv6.2)
cql(include libcql/libfen.cql include libcql/libxfm.cql quiet)
initial

function IsShift(BB1 BB2) {
  retVal = ""
  square hSq in [a-h1,a-h8]
    square vSq in [a1-8,h1-8] {
      hSq ≠ vSq and BB1 and BB1 == Shift(BB2 hSq vSq)
      retVal += str(hSq vSq)
    }
  retVal
}

dictionary CSD0
dictionary CSDT
dictionary SHIFTS[""] = ""  unbind SHIFTS

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 1
  fen2bb(fen)
  unbind CSD0
  string Key in importBB  CSD0[Key] = importBB[Key]
  false
} else {
  fen2bb(fen)
  unbind CSDT
  string Key in importBB  CSDT[Key] = importBB[Key]
  unbind SHIFTS  Count = 0
  // Build the shift profile by piece colortype.
  while ("KQRBNPkqrbnp" ~~ ".") {
    if CSD0[\0] ≠ [] or CSDT[\0] ≠ [] {
      Count += 1
      if not Shifts = IsShift(CSD0[\0] CSDT[\0])
        then Shifts = "Nil"
      if SHIFTS[Shifts]
        then SHIFTS[Shifts] = SHIFTS[Shifts] + \0
        else SHIFTS[Shifts] = \0
    }
  }
  // Find a qualifying entry.
  if #SHIFTS > 1
    string Key in SHIFTS
      if Key ≠ "Nil"  and #(SHIFTS[Key]) > Count * 3 / 5
        SeriesAbort = 0 // and message(\n SHIFTS)
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The general idea in building the board's shift profile is that if we have a near miss, one of the shift signatures will clearly dominate. A few piece types might have a faux signature, and a few will have none. The sweet spot in deciding that we have a sufficient majority seems to be just over half of the piece types.

Symmetries

We wander into yet another one of those places where absurdities rule the day. There are alot of those places in the problem domain, so why stop now?

In the world of compositions, the term "symmetry" has very little to do with it. Any random selection of pieces placed in any random order along any random line is considered to be a symmetric position all onto itself. We're finding that rather difficult to buy into, but, okay, just to keep the peace.

Outside of the twinning domain, a problem is deemed to be asymmetrical if the initial position is symmetrical and the solution (usually the key) busts up the symmetry. Or the initial position may be asymmetrical and the key might move it right into symmetry. Within the twinning domain, we don't care about any of that.

Symmetry in a twinning context begins with a symmetrical board (ill-defined and utterly meaningless) and may or may not include the notion of symmetries across the solutions of the series, which will typically run the entire length of the solutions but may comprise anything that even remotely appears to be a reflection. Again, impossible to define.

Nonetheless, symmetry is a big deal in the problem domain and is probably most interesting in a twinning context, and so here we go.

Board symmetry
The symmetry on the board may manifest about the bisectors, about the diagonals, or about any one of the horizontal or vertical lines not adjacent to an edge (that last part is our own contribution to the warm fuzziness). Most of the compositions construct the symmetry about one of the center ranks or files (mostly files), but a few of the composers just had to be different so they could complicate our lives.

We'll search for a series in which every one of the twins has a symmetrical initial position, regardless of how the twin specifications got us there. Some will rotate through all four orientations, some will flip things about, and some will just throw some pieces around the board. If it makes a happy pattern, it's okay with us.

cql(include libcql/libxfm.cql quiet)
initial

function isSymBisect(BB) {
  BB == Flip(BB a8 h1)
    or
  BB == Flip(BB a1 h8)
    or
  BB == Flip(BB a1 h1)
    or
  BB == Flip(BB a1 a8)
}

function isSymLine(BB) {
  Found = 0
  while ("a1h1a1b1a1h1a1d1a1h1a1f1a1a8a1a2a1a8a1a4a1a8a1a6"
             ~~ "(..)(..)(..)(..)") {
    S1 = makesquare \1  S2 = makesquare \2
    S3 = makesquare \3  S4 = makesquare \4
    if  BB == Shift(Flip(BB S1 S2) S3 S4) or
        BB == Shift(Flip(BB S1 S2) S4 S3)
      then Found = 1
  }
  Found == 1
}

function isSym(BB) {
  isSymBisect(BB) or isSymLine(BB)
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  if not isSym([Aa]) then SeriesAbort = 1
  false
} else {
  if not isSym([Aa]) then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

The only part of the query that might cause some head scratching is the block that looks for symmetry about an arbitrary h- or v-line. It's a quick'n'dirty hack (mostly dirty), remarkably inefficient with resources, an embarrassment for any self-respecting AI. Flip'n'shift magic is all we're going to say about it. Lucky for us, the execution of the search is a one-off and CPU cycles are cheap.
The query will pick up a few interesting critters which may or may not have been intended by the composer as an exercise in symmetry. It would be nearly impossible to filter them out, and they have their own sets of weird little charms, so we won't worry about them. Serendipity.

Solution symmetry
Symmetrical solutions across twins assumes symmetry in the initial positions. The examples that follow should be executed against the matching results from the query above, which has already filtered for board symmetry.
Looking for symmetry across a series of solutions is what we might call "uniquely challenging". Since symmetry in solutions is sometimes in the eye of the beholder, we'll venture into some patterns that may or may not satisfy the purist. The waters become especially murky in the twinning context, as the "symmetric" play may substitute one piece type for another in related play, either through twin specification substitution or through promotion play. Even muddier is the case where thematic play (e.g., self-blocking) becomes intertwined with symmetric play. We're not particularly interested in thematic symmetry, though we'll see some of that along the way.

If the initial position is symmetric, the helpmate is a fairly safe bet as a vehicle for expressing symmetry across the series solutions. We'll focus on the helpmate alone because the solutions are simple and clean, and the queries below are already difficult enough to follow. In particular, the helpmate series with dual solutions per twin is likely to express symmetry across both the dual and across twins, and so is what we might consider to be the apex of solution symmetry artwork. We'll consider duals separately at the tail end of this section.

After studying this class of composition for awhile, one is able to predict fairly accurately which series will incorporate solution symmetry just by a glance at the initial positions and the respective twin specifications. That's the hard way to go about a search in a large database and doesn't help us much in constructing our query.

The easy stuff can be picked out with a fairly straightforward approach. It's so simple that it's difficult to believe how accurate it is. Across the solutions, for every piece type that makes a move in either of the solutions, each type must make the same number of moves across either line of play. We started out thinking that colortype would be the minimum granularity, but it turns out that we can lump both sides together without loss of accuracy. Transposition of moves is commonplace across solutions and so piece type and count are the only criteria that we take into account, as move order bites the dust.

With a slight twist on that approach, we can pull in symmetry where one or two of the pieces in play differ in type across solutions. A twin specification will commonly substitute one type for another (usually exchanging bishop for knight or vice versa), or the type substitution might occur through promotion play. If those correlated pieces satisfy the move count criteria given above, then we likely have some significant degree of symmetry across solutions, though we might need to stare at the solutions (squint, tilt head) for awhile to see it.

First, we'll go after the low hanging fruit. The query matches roughly eighty percent of candidates that actually exhibit some form of symmetry across solutions. The hard stuff follows a bit further below.

// Low hanging solution symmetry.  (CQLv6.2)
cql(include libcql/libhlp.cql quiet variations)
initial

dictionary PT[""] = 0
function RecordMoves() {
  unbind PT  asymCnt = 0
  line primary
    --> {
        not terminal
        fromSq = move from ▦
        fromId = "ID"+str(pieceid fromSq)
        if PT[fromId] or move promote △
          then key = fromId and asymCnt += 1
          else key = str(type fromSq)
        if PT[key]
          then PT[key] = PT[key] + 1
          else PT[key] = 1
        }{*}
  if asymCnt > 0
    then (PT["="] = asymCnt) //and message(PT)
}

dictionary PT0
dictionary PTT

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Stip = tag "Stipulation"
  if not isHelp() or isDual() then SeriesAbort = 1
  RecordMoves()
  unbind PT0   string Key in PT  PT0[Key] = PT[Key]
  false
} else {
  if Stip ≠ tag "Stipulation" then SeriesAbort = 1
  if not isHelp() or isDual() then SeriesAbort = 1
  RecordMoves()
  unbind PTT   string Key in PT  PTT[Key] = PT[Key]
  while ("123456=" ~~ ".")
    if (PT0[\0] or PTT[\0]) and PT0[\0] ≠ PTT[\0]
      then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

As we accumulate the move count per piece type, pawn promotions are handled a bit differently. Since the promoted piece types likely differ, we track the pieces by piece id rather than by type. Differing promoted piece types invariably are at the center of play. If the respective promoted pieces follow up with the same number of moves down their lines of play, then the smell of symmetry is in the air.
Piece substitution in the twin specification can be handled similarly, but with a bit more work. The scheme as implemented should handle multiple promotions per solution, but we've never seen such a beast and don't expect to anytime soon.

We've selected one of the more obvious samples from the matching results as a bit of a tease for things to come. Initial positions are across the top, terminal positions across the bottom. (Open the image in a dedicated tab for full scale.)

One cannot help but notice that something is going on about the anti-diagonal across the terminal positions. Sleeping our way through life as we are, we took note, filed it away, moved along.

The symmetry in play across twins is trivial. The query for the low hanging fruit is constructed precisely toward that end. Things are about to change.

[Event "Кудесник"]
[Site "Yet Another CPDB"]
[Date "2005.09.??"]
[Round "11868600"]
[White "Winokurow, Wadim Konstantinowitsch"]
[Black "H#2 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[SeqNum "11868600"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2"]
[TwinB "Exchange f2 g3"]
[FEN "7K/8/8/4r3/3r4/5kn1/5BR1/b7 b - - 0 1"]

a) 

  1.Rd4-g4 Bf2-d4   2.Re5-e4 Rg2-f2 #

b) wBf2<-->bSg3  

  1.Re5-e2 Bg3-e5   2.Rd4-e4 Rg2-g3 #

And so we began an exercise that was very much like banging one's head against a cinder block wall. Some of the [arguably] symmetric solutions have given us a devil of a time looking for a pattern that might be generalized. We've considered one heuristic after another, with some modest successes but mostly meeting with failure.

Out of ideas, we reluctantly — and against our better judgement — sought out some original insight from the far side (the off-the-farm side) of the family tree:
For those hard cases where the pattern is elusive, don't look for the symmetry directly in play. Look for an indication or suggestion of that symmetry in the respective terminal positions.
```
symmetry across initial positions
    + symmetry across solutions
        => symmetry across terminal positions
```
Bingo. Score one for the unbalanced tree.
Well, okay, not necessarily "symmetry" across terminal positions, but any compound transform of identical piece arrangements (i.e., echo). Is an echo necessarily an indication of symmetric play? Depends on our definition of symmetric play. We can say that echos are very accurate in picking out the hard stuff that had eluded us while looking solely at lines of play, and are also widely on display with the low hanging fruit.

The echos may be derived of any of a plethora of combinations (permutaions) of transform. We've even come across a triple transform (head spinning) which we have no ambitions of matching. We'll test for just a few of the more popular compounds, and leave the rest for the industrious reader.

// Compound transform symmetry.  (CQLv6.2)
cql(include libcql/libhlp.cql include libcql/libxfm.cql quiet variations)
initial

function isFlipShift(BB1 BB2) {
  isShift(BB1 Flip(BB2 a1 h1)) or
  isShift(BB1 Flip(BB2 a1 a8)) or
  isShift(BB1 Flip(BB2 a1 h8)) or
  isShift(BB1 Flip(BB2 a8 h1))
}

function isRotateShift(BB1 BB2) {
  isShift(BB1 Rotate(BB2 "90")) or
  isShift(BB1 Rotate(BB2 "180")) or
  isShift(BB1 Rotate(BB2 "270"))
}

function isRotateFlip(BB1 BB2) {
  isFlip(BB1 Rotate(BB2 "90")) or
  isFlip(BB1 Rotate(BB2 "180")) or
  isFlip(BB1 Rotate(BB2 "270"))
}

function isXF(BB1 BB2 BB3 BB4) {
       if false then true
  else if isShift(BB1 BB2) and isShift(BB3 BB4) and isShift(BB1|BB3 BB2|BB4) then true //and message("shift")
  else if isFlip(BB1 BB2) and isFlip(BB3 BB4) and isFlip(BB1|BB3 BB2|BB4) then true //and message("flip")
  else if isFlipShift(BB1 BB2) and isFlipShift(BB3 BB4) and isFlipShift(BB1|BB3 BB2|BB4) then true //and message("flip'n'shift")
  else if isRotateShift(BB1 BB2) and isRotateShift(BB3 BB4) and isRotateShift(BB1|BB3 BB2|BB4) then true //and message("rotate'n'shift")
  else if isRotateFlip(BB1 BB2) and isRotateFlip(BB3 BB4) and isRotateFlip(BB1|BB3 BB2|BB4) then true //and message("rotate'n'flip")
  else false
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Found = 0
  persistent Stip = tag "Stipulation"
  persistent wOccupied = []
  persistent bOccupied = []
  find { terminal  wOccupied = A  bOccupied = a }
  if not isHelp() or isDual() then SeriesAbort = 1
  false
} else {
  if Stip != tag "Stipulation" then SeriesAbort = 1
  if not isHelp() or isDual() then SeriesAbort = 1
  if find { terminal and isXF(wOccupied A bOccupied a) }
    then Found = 1
  TwinCount -= 1 
  if TwinCount == 0 and SeriesAbort == 0 and Found == 1
    then true
    else false
}

We first tried applying the transforms on boards representing all occupied squares, and should have stopped there. It was almost good enough. Breaking the board out by piece color introduced its own set of problems. Finally we settled on all of the above. Highly accurate, but probably a bridge too far.
To take a look at the matching results for some lesser selection of the compounds tested in the isXF() function, simply comment out the unwanted lines (one compound per line). There will be some crossover in the respective results, and one will notice a healthy representation of the low hanging series in the mix. One can easily separate out the series of interest (the hard stuff) by filtering the results for the low hangers and then negating the game list (a couple of clicks of the mouse within Scid).

As novices in the problem domain, we feel that some of the matching series qualify as "WOW" material. But that's just us. We've picked one of those as a sample, with initial positions across the top and echos across the bottom. (Open the image in a dedicated tab for full scale.)

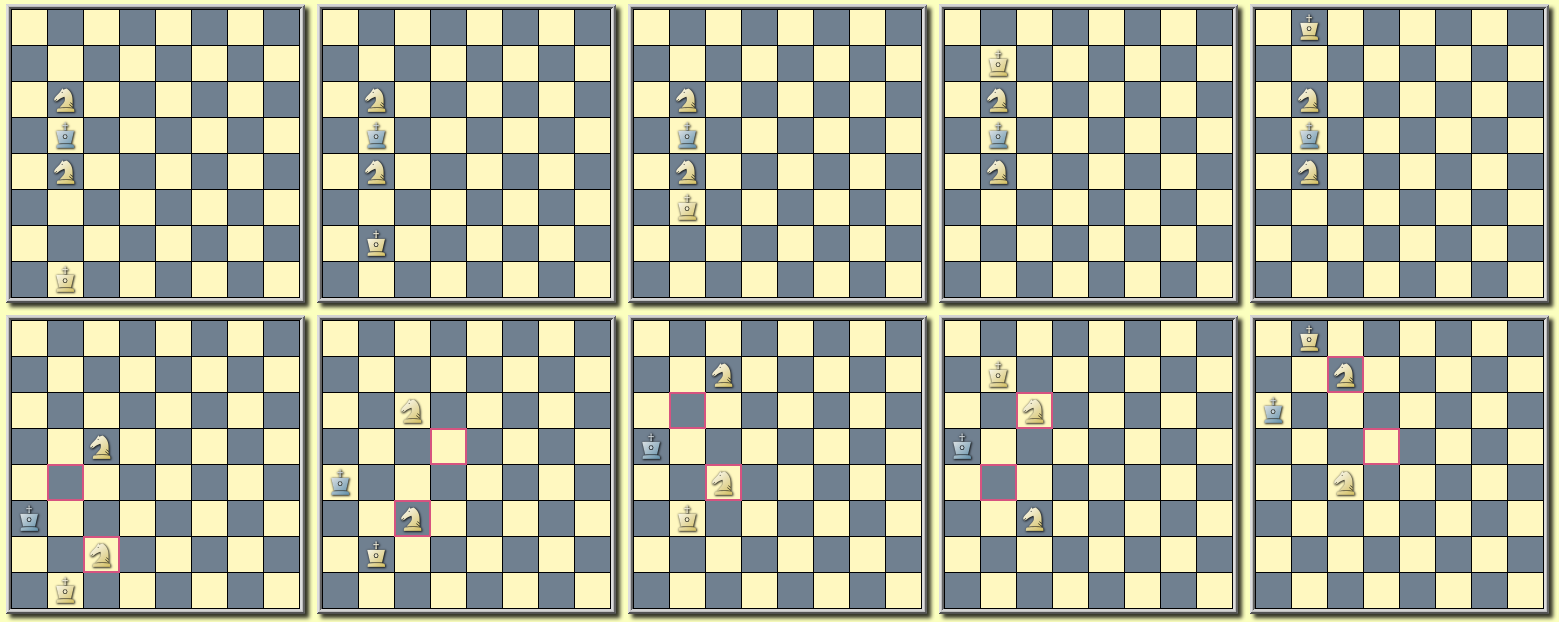
The play across twins in the series is clearly symmetric (unlike most of the matching series), but we chose this composition by Holladay in spite of that. The knights' maneuvering across the series — an exotic choreographed dance taken frame by frame — is especially appealing to us. And, of course, each sequence of steps in the dance echos its mate. We admit that we're easily impressed, but we're overworked and underappreciated and so we take the liberty of humoring ourselves (insert emoticon of choice) at every opportunity.

[Event "Schach-Echo"]
[Site "Yet Another CPDB"]
[Date "1975.10.15"]
[Round "10387800"]
[White "Holladay, Edgar Dinwiddie"]
[Black "H#2.5 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "4"]
[Keywords "Miniature:Rex solus:No pawns:Ideal mates:Chameleon echo mates:King and two knights checkmate"]
[SeqNum "10387800"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#2.5"]
[TwinB "Move b1 b2"]
[TwinC "Move b1 b3"]
[TwinD "move b1 b7"]
[TwinE "Move b1 b8"]
[FEN "8/8/1N6/1k6/1N6/8/8/1K6 w - - 0 1"]


a) 

  1...Sb6-d7   2.Kb5-a4 Sd7-c5 +   3.Ka4-a3 Sb4-c2 #

b) wKb1-->b2  

  1...Sb6-d5   2.Kb5-a5 Sb4-c6 +   3.Ka5-a4 Sd5-c3 #

c) wKb1-->b3  

  1...Sb4-d5   2.Kb5-a6 Sd5-c7 +   3.Ka6-a5 Sb6-c4 #

d) wKb1-->b7  

  1...Sb6-d5   2.Kb5-a4 Sd5-c3 +   3.Ka4-a5 Sb4-c6 #

e) wKb1-->b8  

  1...Sb4-d5   2.Kb5-a5 Sb6-c4 +   3.Ka5-a6 Sd5-c7 #

Twinned helpmates with dual solutions across the series provide a broad canvas for creativity. We nearly bailed out of this example on account of the "pointless exercise" score being so high. Pretty much every series exhibits some form of interesting solution symmetry across both duals and twins. But we decided to play around with it to see what we might discover that would otherwise go unnoticed. We're glad that we did.

Out of the experiment fell a real gem of a composition where the test for symmetry in play fails locally (across duals) but is a clear hit across twins for each of the dual solutions. Icing on the cake stuff includes echos across duals across twins. One can achieve some satisfying effects when the duals are "mated" across twins in such a fashion, and we'll highlight that composition below.

As the query stands, it will match a series that expresses symmetry in play and echos in terminal positions across duals for each twin in the series. The flavor of echo must match across twins. These are more or less arbitrary criteria, but the mechanics for implementing the tests for the criteria are flexible and serve as a decent starting point for the masochist. Some strategic commenting and uncommenting of lines will match various combinations of symmetry for those less inclined to hurt themselves. Enough of that.

// Twins and duals and echoes, oh my.  (CQLv6.2)
cql(include libcql/libhlp.cql include libcql/libxfm.cql quiet variations)
initial

function isFlipShift(BB1 BB2) {
  isShift(BB1 Flip(BB2 a1 h1)) or
  isShift(BB1 Flip(BB2 a1 a8)) or
  isShift(BB1 Flip(BB2 a1 h8)) or
  isShift(BB1 Flip(BB2 a8 h1))
}

function isRotateShift(BB1 BB2) {
  isShift(BB1 Rotate(BB2 "90")) or
  isShift(BB1 Rotate(BB2 "180")) or
  isShift(BB1 Rotate(BB2 "270"))
}

function isRotateFlip(BB1 BB2) {
  isFlip(BB1 Rotate(BB2 "90")) or
  isFlip(BB1 Rotate(BB2 "180")) or
  isFlip(BB1 Rotate(BB2 "270"))
}

function isXF(BB1 BB2 BB3 BB4) {
       if false then true
  else if isShift(BB1 BB2) and isShift(BB3 BB4) and isShift(BB1∪BB3 BB2∪BB4) then typeXF = 1 //and message("shift")
  else if isFlip(BB1 BB2) and isFlip(BB3 BB4) and isFlip(BB1∪BB3 BB2∪BB4) then typeXF = 2 //and message("flip")
  else if isFlipShift(BB1 BB2) and isFlipShift(BB3 BB4) and isFlipShift(BB1∪BB3 BB2∪BB4) then typeXF = 3 //and message("flip'n'shift")
  else if isRotateShift(BB1 BB2) and isRotateShift(BB3 BB4) and isRotateShift(BB1∪BB3 BB2∪BB4) then typeXF = 4 //and message("rotate'n'shift")
  else if isRotateFlip(BB1 BB2) and isRotateFlip(BB3 BB4) and isRotateFlip(BB1∪BB3 BB2∪BB4) then typeXF = 5 //and message("rotate'n'flip")
  else typeXF = 0

  typeXF
}

dictionary PT[""] = 0
function RecordMoves() {
  unbind PT  asymCnt = 0
  line
    --> {
        toSq = move to ▦ previous
        toId = "ID"+str(pieceid toSq)
        if PT[toId] or move promote △ previous
          then key = toId and asymCnt += 1
          else key = str(type toSq)
        if PT[key]
          then PT[key] = PT[key] + 1
          else PT[key] = 1
        }{*}
  if asymCnt > 0
    then (PT["="] = asymCnt) //and message(PT)
}

dictionary PTD1
dictionary PTD2

function isSymPlay(){
  Found = 1
  child(0):RecordMoves()
  unbind PTD1   string Key in PT  PTD1[Key] = PT[Key]
  child(1):RecordMoves()
  unbind PTD2   string Key in PT  PTD2[Key] = PT[Key]
  while ("123456=" ~~ ".")
    if (PTD1[\0] or PTD2[\0]) and PTD1[\0] ≠ PTD2[\0]
      then Found = 0
  Found == 1
}

function isSymEcho() {
  child(0):find { terminal  wOccupiedD1 = △  bOccupiedD1 = ▲ }
  child(1):find { terminal  wOccupiedD2 = △  bOccupiedD2 = ▲ }
  isXF(wOccupiedD1 wOccupiedD2 bOccupiedD1 bOccupiedD2)
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Stip = tag "Stipulation"
  if not (isHelp() and isDual()) then SeriesAbort = 1
  if not isSymPlay() then SeriesAbort = 1
  persistent typeEcho = isSymEcho()
  if typeEcho == 0 then SeriesAbort = 1
  false
} else {
  if not (isHelp() and isDual()) then SeriesAbort = 1
  if Stip ≠ tag "Stipulation" then SeriesAbort = 1
  if not isSymPlay() then SeriesAbort = 1
  if isSymEcho() ≠ typeEcho then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

We probably should point out that we employ the child() filter to help us to distinguish the dual solutions. One line will be in primary play from the initial position and the other in secondary play. Then we record moves leading to a given position rather than from the position as in prior examples because the resulting line bypasses the bifurcating initial position.
As promised, we present [yet another] Holladay composition with symmetry across duals and across twins. Initial positions are on the left, with dual echos to the right of their respective initial positions. Notice that all echos are flip'n'shift, about the horizontal bisectors across duals, the vertical bisectors across twins. (Open the image in a dedicated tab for full scale.)

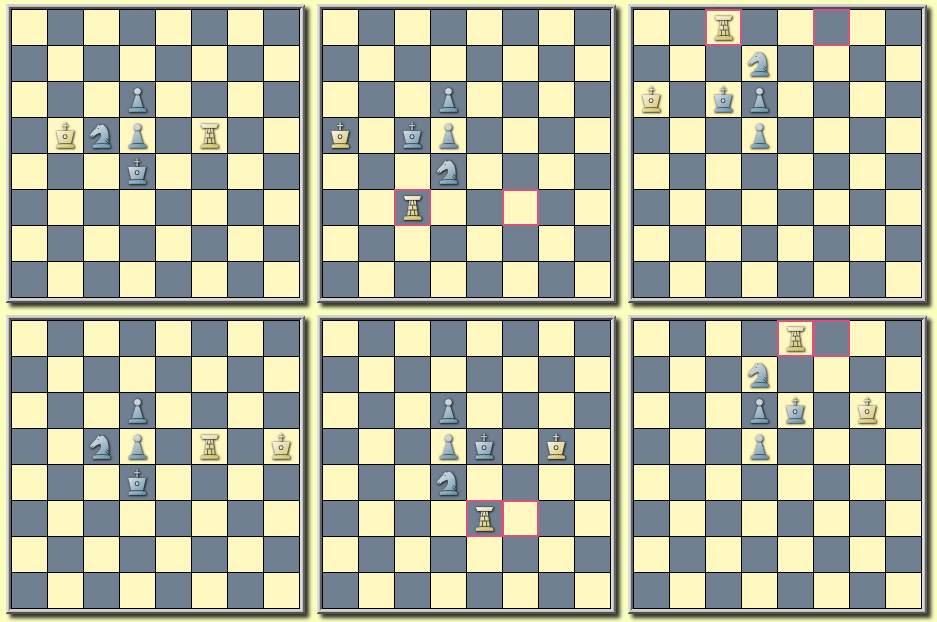
It doesn't take long to spot the symmetry in play, transpositions taken into account. Perhaps not the most original of helpmates, but Holladay gets bonus points for visual effect.

[Event "Ideal-Mate Review"]
[Site "Yet Another CPDB"]
[Date "1985.07.??"]
[Round "10699500"]
[White "Holladay, Edgar Dinwiddie"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[SeqNum "10699500"]
[SetUp "1"]
[Solutions "2.1.1..."]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move b5 h5"]
[FEN "8/8/3p4/1Knp1R2/3k4/8/8/8 b - - 0 1"]

a) 

  1.Sc5-e6 Kb5-a5   2.Kd4-c5 Rf5-f3   3.Se6-d4 Rf3-c3 #
  1.Sc5-d7 Kb5-a6   2.Kd4-c5 Rf5-f8   3.Kc5-c6 Rf8-c8 #

b) wKb5-->h5  

  1.Sc5-b3 Rf5-f3   2.Kd4-e5 Kh5-g5   3.Sb3-d4 Rf3-e3 #
  1.Sc5-d7 Rf5-f8   2.Kd4-e5 Kh5-g6   3.Ke5-e6 Rf8-e8 #

Cyclic patterns

The cyclic theme is quite possibly the most challenging theme for the composer. In a twinning context it ain't no cake walk for the CQL'er, either. We were tempted to avoid the topic, altogether, but our masochistic side got the better of us.

For any reader who is a little bit confounded by the classification system for the cyclic theme, well, one has plenty of company. The singular authority on the subject is probably (arguably) one Peter Gvozdják, author of the Cyclone book. The system he describes is the system we'll use.

The helpmate can express cyclic patterns across multiple solutions (or twins), but we'll avoid those for the time being. We'll stick to the vertical class of the three-phase direct two-mover, where the defenses are the same across twins.

In the interest of simplicity (a term that does not actually apply in this context), we'll part ways with the convention that defines an identical mating move as by the same piece, as opposed to from the same square. For example, a twin specification might move the thematic mating piece to a different square, or the thematic piece might move twice in a three-mover. We're going to stay with the from the same square definition.

Cyclic patterns can be insanely difficult (see the Ukrainian double, for example — series 10824300 and 11000200), but we'll try to keep things relatively sane in the examples that follow. Our approach to matching cyclic patterns across twins borrows from the "what else could it be" school of magic and enlightenment, with a little bit of help from the gods of chance. The reason for this will become clear in our exploration of the Rice cycle.

The Rice cycle
The Rice is probably the simplest of the patterns that we'll consider, so it's a good place to start. For the same two defenses across a 3-series, the cycle in three phases has mates AB → BC → CA.
Since this is our opening salvo on a difficult task, we should take the opportunity to demonstrate how not to approach the problem.
brute force: adj. Describes a primitive programming style, one in which the programmer relies on the computer's processing power instead of using his or her own intelligence to simplify the problem, often ignoring problems of scale and applying naive methods suited to small problems directly to large ones. The term can also be used in reference to programming style: brute-force programs are written in a heavyhanded, tedious way, full of repetition and devoid of any elegance or useful abstraction.
-- catb.org
In other words, don't do it.

The following monstrosity is the perfect example of correctness and thoroughness gone wrong. Totally lacking in imagination. Virtually unreadable. We won't even bother trying to explain it. Because why? Because don't do it.

cql(quiet variations)
initial  wtm

function RecordMoves() {
  line
    --> move primary
    --> currentposition:{
          defenseA = 0  defenseB = 1
          if move null
            then {defenseA = 1  defenseB = 2}
          not child(defenseB + 1)
          child(defenseA):{
            //message("defenseA Solution " Solution)
            if Solution == 1
              then {
                $fromDefenseA = move from . previous
                $toDefenseA = move to . previous
                $fromSolution1MateA = move from .
                $toSolution1MateA = move to .
              } else {
                $fromDefenseA == move from . previous
                $toDefenseA == move to . previous
              }
            if Solution == 2
              then {
                $fromSolution2MateA = move from .
                $toSolution2MateA = move to .
              }
            if Solution == 3
              then {
                $fromSolution3MateA = move from .
                $toSolution3MateA = move to .
              }
          }
          child(defenseB):{
            //message("defenseB Solution " Solution)
            if Solution == 1
              then {
                $fromDefenseB = move from . previous
                $toDefenseB = move to . previous
                $fromSolution1MateB = move from .
                $toSolution1MateB = move to .
              } else {
                $fromDefenseB == move from . previous
                $toDefenseB == move to . previous
              }
            if Solution == 2
              then {
                $fromSolution2MateB = move from .
                $toSolution2MateB = move to .
              }
            if Solution == 3
              then {
                $fromSolution3MateB = move from .
                $toSolution3MateB = move to .
              }
          }
        }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Solution
  persistent $fromDefenseA
  persistent $toDefenseA
  persistent $fromDefenseB
  persistent $toDefenseB
  persistent $fromSolution1MateA
  persistent $toSolution1MateA
  persistent $fromSolution1MateB
  persistent $toSolution1MateB
  persistent $fromSolution2MateA
  persistent $toSolution2MateA
  persistent $fromSolution2MateB
  persistent $toSolution2MateB
  persistent $fromSolution3MateA
  persistent $toSolution3MateA
  persistent $fromSolution3MateB
  persistent $toSolution3MateB
  if not child  // base is a zeroposition
    then {
      Solution = 0
      if TwinCount != 3 then SeriesAbort = 1
    } else {
      Solution = 1
      if TwinCount != 2 then SeriesAbort = 1
      if not RecordMoves() then SeriesAbort = 1
    }
  false
} else {
  Solution += 1
  if not RecordMoves() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and ({ $fromSolution1MateA == $fromSolution3MateB
             $toSolution1MateA == $toSolution3MateB
             $fromSolution2MateA == $fromSolution1MateB
             $toSolution2MateA == $toSolution1MateB
             $fromSolution3MateA == $fromSolution2MateB
             $toSolution3MateA == $toSolution2MateB }
                 or
           { $fromSolution1MateA == $fromSolution2MateB
             $toSolution1MateA == $toSolution2MateB
             $fromSolution3MateA == $fromSolution1MateB
             $toSolution3MateA == $toSolution1MateB
             $fromSolution2MateA == $fromSolution3MateB
             $toSolution2MateA == $toSolution3MateB })
    then {
/*
      message($fromSolution1MateA $toSolution1MateA " "
              $fromSolution1MateB $toSolution1MateB " "
              $fromSolution2MateA $toSolution2MateA " "
              $fromSolution2MateB $toSolution2MateB " "
              $fromSolution3MateA $toSolution3MateA " "
              $fromSolution3MateB $toSolution3MateB)
*/
      true
    } else false
}

We'll only point out that we rely on the solving engine's consistency in the order in which it considers moves when searching for solutions. Is that a cheat? Yes. Tough. The query is already ugly enough.
Aside from the ugliness and the complexity and the need for an entire array of variable names born of banality (and did we mention the drudgery), this approach does not scale well.

There must be a better way.

Abstraction. Distillation. Simplification. Useful tools in any complex endeavor. What is there about the Rice pattern that might lend itself to the application of these tools?

The first thing we notice is that the respective defensive lines all have the same moves. Same moves == same set of squares from which and to which each of the moves is made. Do we really need to take into account the from and to properties of the moves? Or is it enough just to compare one complete set of squares for one solution with that of another? How many false positives will we incur, and does it really matter when this distillation is taken in concert with the other simplifications we'll employ, all of it across a 3-series?

With a nod to the gods of chance, we give it a try with the query below.

cql(quiet variations)
initial  wtm

function SameDefense() {
  {Count=0  line --> move primary --> move to ~k and Count+=1  Count==2}
  if not $dSquares
    then $dSquares =  child:{move to ~k | move from . to ~k}
    else $dSquares == child:{move to ~k | move from . to ~k}
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $dSquares = ~.
  if not child  // base is a zeroposition
    then {
      if TwinCount != 3 then SeriesAbort = 1
    } else {
      if TwinCount != 2 then SeriesAbort = 1
      if not SameDefense() then SeriesAbort = 1
    }
  false
} else {
  if not SameDefense() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then {
      true
    } else false
}

Much to our surprise, the query draws down the number of eligible series to just sixty out of a database of 6000+ candidates. We notice some reciprocals among them, and a few doubled-up cyclicals that normally would cycle over a single defense. But this result is encouraging. And we haven't even begun to address shifting mates.

So, if it's good enough for the defenses, why not for the mates? Do we really need to take into account the from and to properties of the mating moves? For that matter, do we even need to single out the individual moves? Why not just throw all of the squares into a single set respective of the defensive line. The sets for the two lines should be identical. That is a necessary condition for a match, but is it sufficient to distinguish this pattern from other similar patterns?

Spoiler alert from the school of magic and enlightenment...

cql(quiet variations)
initial  wtm

function RecordMoves() {
  if not $dSquares
    then $dSquares =  child:{move to ~k | move from . to ~k}
    else $dSquares == child:{move to ~k | move from . to ~k}
  Count = 0
  line
    --> move primary
    --> move to ~k and Count += 1
    --> {
        if (Switch % 2) == 0
          then $cSquaresEven = $cSquaresEven | move to . | move from .
          else $cSquaresOdd  = $cSquaresOdd  | move to . | move from .
        Switch += 1
        }
    --> terminal
  Count == 2
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent Switch = 0
  persistent $dSquares = ~.
  persistent $cSquaresEven = ~.
  persistent $cSquaresOdd = ~.
  if not child  // base is a zeroposition
    then {
      if TwinCount != 3 then SeriesAbort = 1
    } else {
      if TwinCount != 2 then SeriesAbort = 1
      if not RecordMoves() then SeriesAbort = 1
    }
  false
} else {
  if not RecordMoves() then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and $cSquaresEven == $cSquaresOdd
    then {
      //message($dSquares $cSquaresEven $cSquaresOdd)
      true
    } else false
}

Not one false positive. Not one. Sometimes we just get lucky.
The RecordMoves() function actually does more than record the moves. It also verifies that the defensive moves are the same across twins and that there are exactly two defensive lines, making a point not to count threat lines.

The third constituent of the line filter might cause some head-scratching at first. Does anyone remember linearization? The question is, "Which defensive line are we on?" Remembering the cheat that we pointed out above, the ordering of the lines is consistent across twins and so we can reliably gather the thematic mating moves into their respective sets without even looking at the defensive moves.

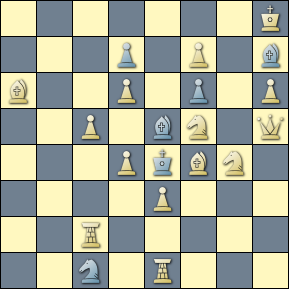Why the modulus-oriented switch? Aside from the fact that the operator is unjustly neglected and dissed in any language (and we hate that), we started out wanting to take duals into account. Bad form, bad idea — cyclics should never have duals (some do). But we left the switch in there just in case we come up with another bad idea. Remnants of brain dysfunction never go away.

The composition by Mojkin qualifies as both a Rice and a Ukrainian double. One has to wonder if this was intentional or just a happy accident. In either case, it's an impressive accomplishment.

[Event "Special Prize, Советский Сахалин"]
[Site "Yet Another CPDB"]
[Date "1989.??.??"]
[Round "10824300"]
[White "Mojkin, Wladimir N."]
[Black "#2 -- Twins -- Actual+Virtual+Set Play"]
[Result "1-0"]
[BlackElo "2"]
[Keywords "Ukrainian double"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#2"]
[TwinB "Move c2 b8"]
[TwinC "Move c2 g7 move f5 d8"]
[FEN "7K/3p1P1b/B2P1p1P/2P1bN1Q/3PkBN1/4P3/2R5/2n1R3 w - - 0 1"]


a) 

   1.Sf5-g7 ! threat:
          2.Qh5-h1 #
      1...Ke4-f3
          2.Sg4*f6 #
      1...Ke4-d5
          2.Ba6-b7 #


b) wRc2-->b8  

   1.Rb8-e8 ! threat:
          2.Sg4*f6 #
      1...Ke4-f3
          2.Ba6-b7 #
      1...Ke4-d5
          2.Qh5-h1 #


c) wRc2-->g7  wSf5-->d8  

   1.Re1-d1 ! threat:
          2.Ba6-b7 #
      1...Ke4-f3
          2.Qh5-h1 #
      1...Ke4-d5
          2.Sg4*f6 #

The Ukrainian cycle
Explanation...

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...
Explanation...

The Ceriani cycle
Explanation...

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...
Explanation...

The Reeves cycle
Explanation...

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...
Explanation...

Reciprocal patterns

When we first embarked on this experiment in the application of CQL in the twinning world, our expectation was that the reciprocals would prove to be considerably easier than the cyclicals. After all, on first inspection one might mistake them for little more than light weight cyclics. After examining a few of the reciprocal themes in a twinning context, we've arrived at a very different impression.

Probably the most common of the reciprocal patterns involves the reversal of mates versus some two same defenses expressed across two phases of play (or twins). But there are more variations on the reciprocal theme than Paganini could shake a stick at, and the entire class of themes (we are learning) is a fascinating world unto itself. In particular, the reciprocal exchange of function or role between pieces is especially rich and varied — and probably presents the greatest challenge to us — so we'll take a stab at a few of those.

Most of the themes that we'll consider below (both direct and help) may be doubled-up into some rather spectacular specimens, and we'll make a point of directing some of the queries toward those doubles. It should not surprise us that examples of many of the themes are rare in the twinning world and are hard to come by, but we've tried to find a sample on the net to add to the twins database for test purposes.

Having taken on the cyclic patterns in the previous section, the plain vanilla reciprocal mate is trivial by comparison and is hardly worthy of our attention. But we'll begin by looking at one of the more popular (and slightly less trivial) mate changes, which comes with a minor twist.

The le Grand
While the typical reciprocal exchange of mates is between two thematic defenses, the le Grand is an exchange between a threat and a single defense. The reciprocal pattern is normally expressed between some phase in virtual play and lines in post-key play. When the pattern is expressed across twins, all lines are post-key.

cql(quiet variations)
initial  wtm

function RecordMoves(threat defense _mate) {
  line --> move primary --> move null
       --> threat = threat | move from . | move to .
  line --> move primary --> not move null
       --> {
           defense = defense | move from . previous | move to . previous
           _mate = _mate | move from . | move to .
           }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $threatA = ~.
  persistent $defenseA = ~.
  persistent $mateA = ~.
  persistent $threatB = ~.
  persistent $defenseB = ~.
  persistent $mateB = ~.
  RecordMoves($threatA $defenseA $mateA)
  if TwinCount != 1 or find {terminal  ply > 3} then SeriesAbort = 1
  false
} else {
  RecordMoves($threatB $defenseB $mateB)
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and $threatA in $mateB
      and $threatB in $mateA
      and 2 <= $defenseA == $defenseB <= 2
      and $defenseA & $defenseB == 2
    then true
    else false
}

We're interested in what we might call a "pure" le Grand two-mover, in which there is but one defensive line in actual play. The conditions given at end-of-series are very accurate in that regard, but the query just happens to also pick up a special case of a king's pseudo le Grand, in which the twin specification moves the king to an adjacent square from which the defensive move is reversed.
A couple of notes on the RecordMoves() function. A null move in the primary line of play is indicative of a key with a threat. For other post-key lines, we record all defensive moves (from and to squares) and all resulting mates in their same respective set variables. Remember that linearization separates out each individual line.

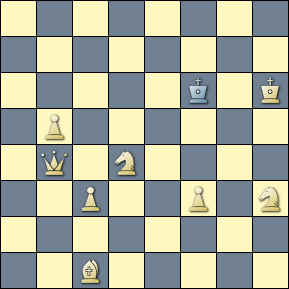One can easily adjust the upper and lower bound on the number of squares recorded in post-key defenses having multiple lines — potentially trading off a bit of accuracy — allowing us to match a le Grand that might include additional thematic components. For example, with an upper and lower bound of three, we find the following king's pseudo le Grand by Nagowizyn which also gives us some paradoxical Dombrovskis.

[Event "Special Comm., Гравюра"]
[Site "Yet Another CPDB"]
[Date "2019.??.??"]
[Round "12767600"]
[White "Nagowizyn, Eduard Nikolajewitsch"]
[Black "#2 -- Twins -- Actual+Virtual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Dombrovskis:Dombrovskis sixfold:Pseudo Le Grand"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "#2"]
[TwinB "Move f6 e5"]
[FEN "8/8/5k1K/1P6/1Q1N4/2P2P1N/8/2B5 w - - 0 1"]


a) 

   1.Bc1-a3 ! threat:
          2.Qb4-e7 #
      1...Kf6-e5
          2.Qb4-d6 #
      1...Kf6-f7
          2.Qb4-f8 #

   1.Sh3-g5 ? threat:
          2.Qb4-d6 #
    but
      1...Kf6-e5 !

   1.Bc1-f4 ? threat:
          2.Qb4-f8 #
    but
      1...Kf6-f7 !

   1.f3-f4 ? threat:
          2.Qb4-f8 #
    but
      1...Kf6-f7 !


b) bKf6-->e5  

   1.Bc1-a3 ! threat:
          2.Qb4-d6 #
      1...Ke5-f6
          2.Qb4-e7 #
      1...Ke5-d5
          2.Qb4-c5 #

   1.Sh3-f4 ? threat:
          2.Qb4-e7 #
    but
      1...Ke5-f6 !

   1.Bc1-g5 ? threat:
          2.Qb4-c5 #
    but
      1...Ke5-d5 !

   1.Kh6-g5 ? threat:
          2.Qb4-c5 #
    but
      1...Ke5-d5 !

   1.Kh6-g7 ? threat:
          2.Qb4-c5 #
    but
      1...Ke5-d5 !

   1.Kh6-g6 ? threat:
          2.Qb4-c5 #
    but
      1...Ke5-d5 !

Exchange of moves
The reciprocal exchange is by a side (white or black) with two moves being swapped at the same two ply across phases. The moves are not necessarily consecutive for the side. The pattern is typically seen across multiple solutions in helpmates, but is also common in the twinning domain. The theme may be doubled up for a side or solutions may express the theme for both sides simultaneously.
We're moving into some new territory now with regard to language technique. The pattern requires that we maintain a correlation between move and ply across twins. CQL provides no natural means for maintaining such a relationship, a mapping for which we would usually seek out an indexable data structure. But we do have the bitboard in the guise of a set variable, a flexible critter where the setting and clearing of bits can mean whatever we want it to mean.

If we look on the bitboard as a general purpose 8x8 matrix (ever thankful for 64-bit architectures), we have two dimensions to work with which allows us to index into the "array" along one of those dimensions while recording information across the other. If we are using ply as the index, then we have our correlated data store. Fortunately, the slice of eight bits at each index maps nicely to the dimensions of a chess board.

So what information do we need to carry across twins in our data store? As relates to a move at a particular ply of a solution, we'll probably be needing (in some form) the properties of from-ness and to-ness for both rank and file. Typically, we would just separate out information across however many bitboards we need until we've achieved a granularity that satisfies the gods of chance. We'll employ a similar strategy, here, while still maintaining that all-important correlation of ply and move.

We'll use two bitboards per solution to carry the moves' file and rank info, the from-ness and to-ness of a particular move recorded on both boards at the same index. The index into an array for any given move is determined by the move's ply. So, for the move Ne5-d3 at ply one, the move would map as [d1,e1] and [c1,e1] for the respective bitboards (file and rank). If the move were at ply two, change all ones to twos. The mapping of a move to the two boards makes extensive use of the rank, file and makesquare filters.

A word or two about false positives might be in order, since the query as given below picks up a few of those. We could easily have eliminated all of them by doubling the number of bitboards employed per solution and doubling the length of the query, but that would only make the code harder to read and with very little to gain. An even better reason for leaving the false positives in the result is that they tend to be considerably more thematically interesting than the patterns that we're ostensibly looking for. Who knew?

cql(quiet)
initial   btm or player black ".5"

// From and to squares go to the same bitslice; file and rank are mapped
// into separate bitboards by ply.
function mapMove(fbp rbp) {
  fbp = fbp | makesquare(file move from .  ply+1)
            | makesquare(file move to .    ply+1)
  rbp = rbp | makesquare(rank move from .  ply+1)
            | makesquare(rank move to .    ply+1)
}

// For a slice of the matrices (moves by ply), do the moves'
// ranks/files match?
function hasMatch(bbA bbB) {
  bbA == bbB > 0
  square all SquareA in bbA
    square SquareB in bbB {file SquareA == file SquareB}
}

// Nested loops find matching moves and record a mapping of the
// respective indices.  If we "fold" the mapping of matching moves
// at the major diagonal bisector, then we can detect reciprocity
// in move exchanges at the intersection of mappings.  Any mapping that
// lies ON the bisector is a fair indication that the series
// is not what we're looking for, and the series match is aborted.
function hasPattern() {
  matchMap = ~.
  IndexA = 0
  loop {
    FileA = $fileByPlyA & up IndexA a-h1
    RankA = $rankByPlyA & up IndexA a-h1
    IndexB = 0
    loop {
      FileB = $fileByPlyB & up IndexB a-h1
      RankB = $rankByPlyB & up IndexB a-h1
      if hasMatch(FileA FileB) and hasMatch(RankA RankB)
        then matchMap = matchMap | makesquare(IndexA+1 IndexB+1)
      IndexB += 1
      IndexB < 8
    } // inner loop
    IndexA += 1
    IndexA < 8
  } // outer loop
  Count = 0
  square Square in matchMap
    if file Square == rank Square
      then SeriesAbort = 1
      else if makesquare(rank Square  file Square) & matchMap
             then Count += 1
  sort "Exchanges" Count / 2
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $fileByPlyA = ~.
  persistent $rankByPlyA = ~.
  persistent $fileByPlyB = ~.
  persistent $rankByPlyB = ~.
  line --> mapMove($fileByPlyA $rankByPlyA){*}
  if TwinCount != 1 then SeriesAbort = 1
  false
} else {
  line --> mapMove($fileByPlyB $rankByPlyB){*}
  TwinCount -= 1
  if TwinCount == 0 and hasPattern() > 1 and SeriesAbort == 0 
    then {
      //message($fileByPlyA $rankByPlyA)
      //message($fileByPlyB $rankByPlyB)
      //message(matchMap)
      true
    } else false
}

One of the first things that might occur to one is that this scheme only handles solutions with up to eight ply. With a little bit of work we could double that by separating out ply by side-to-move. After all, the pattern expresses on a side-to-move basis. But, honestly, who can solve a helpmate with more than eight ply in any event? And we ignore the side-to-move criteria, anyways. Conclusion? Eight is good enough for demonstration purposes.
Secondly, one might have noticed that we limit the result to matching series that double down on the theme. The straight-up pattern is so common as to be unremarkable, and doubling reduces the odds of hitting the trivial false positive.

In trying to visualize the mechanics that are at play in the query above, it helps (trust us) to uncomment the message filters that dump the bitboards to stdout. With the solving engine's solutions at hand, the "folding" of the matchMap board at the diagonal bisector comes into clear focus.

We've chosen to present the following matching helpmate by Winokurow, not just because it expresses the pattern for both sides in six ply, but because it also throws in reciprocal capture-tracebacks that are reported (falsely) as a triple hit. We like it when being so wrong can be so right.

[Event "MT Aleksandr Baturin-100"]
[Site "Yet Another CPDB"]
[Date "2009.??.??"]
[Round "12153200"]
[White "Winokurow, Wadim Konstantinowitsch"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Move b2 g2"]
[FEN "6K1/2p1p3/2P1P1R1/3brpp1/B1p1kprn/2pp4/1PqP4/8 b - - 0 1"]


a) 

  1.Re5*e6 b2*c3   2.Re6-e5 + Rg6-e6   3.Bd5*c6 Ba4*c6 #

b) wPb2-->g2  

  1.Bd5*c6 d2*c3   2.Bc6-d5 Ba4-c6   3.Re5*e6 Rg6*e6 #

The Bristol
The reciprocal Bristol (a line clearance theme) has the same two pieces exchanging their roles across phases (or twins). The pattern may be bi-color and — in a twinning context — is most commonly found in the helpmate. According to some, the purity of the theme depends on the clearing piece having no role in follow-on play (e.g., giving or supporting mate). We'll not concern ourselves with that particular doctrine.
Rather than reinvent a perfectly good wheel design, we've shamelessly ripped off the Bristol example from the online reference (with some minor edits) to carry out our pattern recognition function. This is not what one would consider a difficult query, and is therefore probably a good place to start with our exchange-of-role class of reciprocals.

cql(quiet)
initial

function hasPattern(back front) {
  Start = currentposition
  piece Front in [QRBqrb]
    piece Back in [QRBqrb]
      line
        --> .*
        --> move from Front
        --> .*
        --> {
            xray(Back between(Start:Front Front) Front)
            move from Back to anydirection Front
            back = Start:Back  front = Start:Front
            } 
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $backA = ~.
  persistent $frontA = ~.
  persistent $backB = ~.
  persistent $frontB = ~.
  if not hasPattern($backA $frontA) then SeriesAbort = 1
  if TwinCount != 1 then SeriesAbort = 1
  false
} else {
  if not hasPattern($backB $frontB) then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and $backA == $frontB and $backB == $frontA
    then true
    else false
}

We allow for a white, black or bi-color Bristol and do not require that the moves are consecutive or that the critical square is adjacent to the clearing piece. In fact, the query will match a pattern where the thematic pieces are not even aligned in the starting position.
The helpmate by Siotis is fairly typical of the Bristol, the thematic pieces doing their best to take themselves out of play. This problem even we might be able to solve on a good day.

[Event "The Problemist Supplement"]
[Site "Yet Another CPDB"]
[Date "1997.01.??"]
[Round "11242700"]
[White "Siotis, Nikos"]
[Black "H#3 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3"]
[TwinB "Exchange d5 a6"]
[FEN "bB2K3/p1p5/pqp5/krpn4/r1n5/2pp4/1R2P3/2b5 b - - 0 1"]


a) 

  1.Rb5*b2 e2*d3   2.Qb6-b3 d3*c4   3.Sd5-b4 Bb8*c7 #

b) bSd5<-->bPa6  

  1.Qb6*b8 + Ke8-d7   2.Rb5-b7 Kd7*c6   3.Sc4-b6 Rb2-b5 #

Reciprocal batteries
Two line pieces of different type (e.g., rook and bishop) form batteries in which they exchange roles across twins. This pattern makes a particularly striking impression when doubled and especially with reciprocity realized across the double, as well.
The query will seem vaguely familiar, having just reviewed the Bristol above. The difference, of course, is that we are looking exclusively for the very cool double battery formation, which we feel warrants the redundant waste of space. By the way, searching for reciprocal single formations requires just a couple of edits and will also pick up the doubles.

cql(quiet)
initial  btm or player black ".5"

function hasPattern(back front) {
  piece Front in [RB]
    piece Back in [RB]
      line
        --> .*
        --> xray(Back Front k) and move from Front
        --> Back attacks k
        --> .*
        --> xray(Front Back k) and move from Back
        --> {
            Front attacks k
            front = position 0:Front  back = position 0:Back
            }
}

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  persistent $backA = ~.
  persistent $frontA = ~.
  persistent $backB = ~.
  persistent $frontB = ~.
  if not hasPattern($backA $frontA) then SeriesAbort = 1
  if TwinCount != 1 then SeriesAbort = 1
  false
} else {
  if not hasPattern($backB $frontB) then SeriesAbort = 1
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
      and $backA == $frontB and $backB == $frontA
    then true
    else false
}

We find that this doubled up pattern is most likely to manifest in the helpmate. One suspects that might have something to do with the convenient assist from the black king as he deliberately steps into the batteries once they have formed.
That assist is demonstrated across all of the batteries constructed in the composition by Jonsson and Wiehagen. The black king is being quite helpful on his way to the gallows.

[Event "Die Schwalbe"]
[Site "Yet Another CPDB"]
[Date "1996.08.??"]
[Round "11194200"]
[White "Jonsson, Bernt Christer & Wiehagen, Rolf"]
[Black "H#3.5 -- Twins -- Actual Play"]
[Result "1-0"]
[BlackElo "1"]
[Keywords "Reciprocal interference:Play on same square:Battery play"]
[SetUp "1"]
[Solver "Popeye v4.85"]
[Stipulation "H#3.5"]
[TwinB "Move d2 c3"]
[FEN "8/3p4/3p2K1/8/3n4/6n1/3k2P1/4RB2 w - - 0 1"]


a) 

  1...Bf1-e2   2.Kd2-e3 Be2-d1 +   3.Ke3-f4 Re1-e2   4.Kf4-g4 Re2-e4 #

b) bKd2-->c3  

  1...Re1-e2   2.Kc3-c4 Re2-e1 +   3.Kc4-d5 Bf1-e2   4.Kd5-e6 Be2-c4 #

The Zilahi
A helpmate theme in which two white pieces exchange function across two phases of play (or twins). That functional change might be, e.g., guarding or mating versus being captured.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...

Reciprocal capture
Two pieces exchange their active (capturing) and passive (captured) role between phases (twins), commonly doubled-up.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...

Change of continuation
Reciprocal exchange of lines of continuation, with interchange of one or more moves. (See the Tura theme for an extreme example.)

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...

The Indian
The Indian was apparently an Sam Loyd obsession for a period, and he is given credit (blame) for defining what does and does not qualify. In his own words:
It is a three-move theme: first, the withdrawal of a piece, the critical move; second, its ambush to prevent a stalemate; and finally the mate. The term 'discovered mate' is not used, because the mate may be effected without it; but the prevention of stalemate is absolutely essential.
Depending on who you talk to, Loyd got it all wrong.
For some, discovery is an essential part of the theme. For others, the threat of stalemate is not relevant. About the only points of agreement are that: 1) the key gives us the critical withdrawal (and the further out of play the better), 2) the ambush manifests as interference on the critical square (which may or may not prevent a stalemate), and 3) mate is given with a move off of the critical square (with or without discovery).

We tend to agree with Loyd on the stalemate angle, else what's the point of the ambush. As for discovered mate, the theme feels more cohesive with than without.

cql(quiet)
initial

if player black "Twins"
then {
  persistent TwinCount = elo black
  persistent SeriesAbort = 0
  false
} else {
  TwinCount -= 1
  if TwinCount == 0 and SeriesAbort == 0
    then true
    else false
}

Explanation...

Credits

This document is Copyright (c) 2019-2024 Lionel Hampton. The Chess Query Language was originally developed by Gady Costeff and Lewis Stiller. The upstream Scid vs PC project is managed by Steven Atkinson.

The diagrams appearing in this document were created with the Scid vs PC application's board screenshot facility. The piece set is included with that application and is credited on the project's site.

The composite tiled diagrams (multiple boards on a grid) are the product of the montage command line utility packaged with the ImageMagick tool chest.