Understanding Sets in a CQL Universe

This document (still under development) is a companion to the CQL by Example document presented on the Scid++ project site. A reviewer of the mainline document suggested this one, observing that the difficulty in visualizing complex set operations is the most significant obstacle to getting one's head around CQL. Given the fundamental relationship between CQL and sets, the author found that argument compelling... and so here we are.

We assume that the reader is unschooled in set theory and cares even less about mathematics in general. But CQL's application is in the context of the game of chess, after all, and so we shall endeavor to instill an appreciation of the power and of the esthetic beauty inherent in the relationships between sets on the board. Operations on sets are at the very heart of CQL.

A [very] brief introduction to set theory

Set theory is a branch of mathematics that studies, in lay terms, the collection of objects. For our purposes, we are interested in the collection of squares on a chess board. The theory of sets begins with the binary relation between an object and a set; i.e., an object either is or is not a member of the set. The set is also an object and so we can have a relation (subset) between sets.

Just as there are operations defined on numbers (addition, subtraction), set theory defines certain operations on sets. And, as operations on numbers produce a number, operations on sets likewise produce a set. Of the set theoretic operations, CQL has implemented several:

  1. The union of two sets is the set of all objects that are a member of one or both of those sets.
  2. The intersection of two sets is the set of all objects that are members of both of those sets.
  3. The complement of a set is the set of all objects that are not a member of that set.

Beyond CQL's set theoretic operators, many of CQL's filters operate on sets and yield a set as a result. We should note that any set operation may yield an empty or null set, which has no members.

Examples of set operations

Since visualization is the whole point of this document, chess diagrams will be found throughout. In addition, each of the following examples includes the CQL syntax that yields the collection of sets depicted in its respective diagram.

If uncertain about the set resulting from a set operation or a set filter, add the expression to a comment filter to get a readout of the elements of the set (see the subset example below). Also see the reference manual with regard to the message filter.

The basics

The examples in this section employ CQL attack filters to generate sets that serve as arguments for the set operations demonstrated. The attack fields are marked by colored circles and the set resulting from the operation is marked by a solid disc or square. In addition to the visual depiction of those sets on the board, a textual readout is given as it is rendered by the CQL comment filter.

  • Intersection of sets
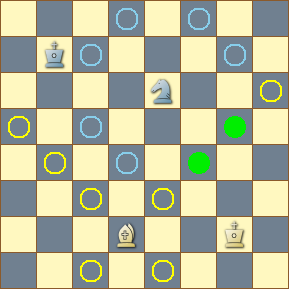  • The position depicted in the diagram shows a knight and a bishop on the board and marks the squares in the attack fields of each piece, as well as the squares that are at the intersection of those sets. The CQL operator employed for set intersection is the lowly ampersand.
    The CQL expression . attackedby B & . attackedby n yields all three of the sets in the diagram. The CQL comment filter gives us:
    • [c1,e1,c3,e3,b4,f4,a5,g5,h6] for the bishop attack field,
    • [d4,f4,c5,g5,c7,g7,d8,f8] for the knight attack field, and
    • [f4,g5] for the result of the intersection operator.

  • Union of sets
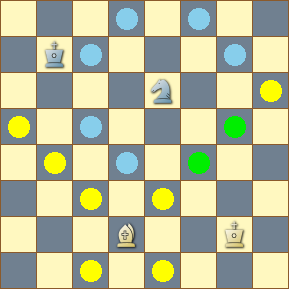  • Same knight. Same bishop. But the operation depicted is of the union of two sets, and the CQL operator is the vertical bar.
    The CQL expression . attackedby B | . attackedby n yields all three of the sets in the diagram. The CQL comment filter gives us:
    • [c1,e1,c3,e3,b4,f4,a5,g5,h6] for the bishop attack field,
    • [d4,f4,c5,g5,c7,g7,d8,f8] for the knight attack field, and
    • [c1,e1,c3,e3,b4,d4,f4,a5,c5,g5,h6,c7,g7,d8,f8] for the result of the union operator.

  • Complement of a set
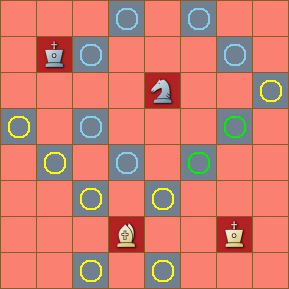  • The diagram depicts the complement of the union of three sets: the attack fields for the knight and bishop as above, and the set of all the squares occupied by a piece. The CQL operator for the complement of a set is the tilde character.
    The CQL expression ~(. attackedby B | . attackedby n | [Aa]) yields all four of the sets in the diagram. The CQL comment filter gives us:
    • [c1,e1,c3,e3,b4,f4,a5,g5,h6] for the bishop attack field,
    • [d4,f4,c5,g5,c7,g7,d8,f8] for the knight attack field,
    • [d2,g2,e6,b7] for the pieces on the board, and
    • [a1,b1,d1,f1,g1,h1,a2,b2,c2,e2,f2,h2,
      a3,b3,d3,f3,g3,h3,a4,c4,e4,g4,h4,
      b5,d5,e5,f5,h5,a6,b6,c6,d6,f6,g6,
      a7,d7,e7,f7,h7,a8,b8,c8,e8,g8,h8]
      for the result of the complement operator.

  • The subset
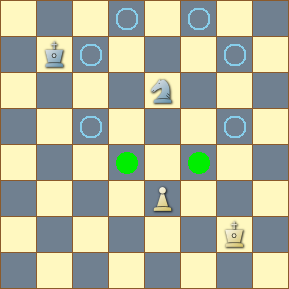  • The subset relation between two sets is a binary relation in which all members of one set are also members of the other set. Members of the subset are all at the intersection of the two sets. In the diagram, the set of squares in the pawn's field of attack is a subset of the set in the field of the knight.

    The following compound filter matches the position of the diagram only because the attack field of the pawn is a subset of the attack field of the knight. The sets representing those fields are assigned to their respective variables. Note that we must stipulate that the Pawn set is not empty because an empty set is a subset of every set. Thus, if there is a white pawn on the board and the subset clause is true (Pawn in Knight), the operational set is assigned the set of squares at the intersection of the two fields (Pawn & Knight). 

  • cql() 
  Knight = . attackedby n
  Pawn = . attackedby P
  Pawn and Pawn in Knight and OpSet = Pawn & Knight
  comment (Knight "  " Pawn "  " OpSet)

Theory in practice

In theory, theory and practice are the same. In practice, they are not.

  • Isolated pawns
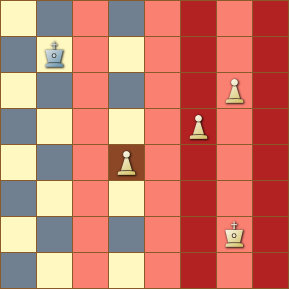  • The diagram shows three white pawns, one of which is isolated and two of which are not. The CQL expression P & ~(horizontal 1 vertical 0 7 P) matches the position through the application of set theoretic operations on a union of sets.

    Dissecting the expression, the primary set generating mechanism is the CQL sub-expresssion in parens — the nested direction filters — which effectively gives us the union of the sets generated by that filter for each white pawn on the board. The filter vertical 0 7 P gives us a set including every square on every file on which there is a white pawn. Thus, the whole of the filter nest horizontal 1 vertical 0 7 P gives us every square on every file adjacent to a white pawn. That set is depicted as the alternating colored files in the diagram.

    Taking the complement of that set, we have the set of all squares that are not on a file adjacent to a white pawn. Finally, at the intersection of that complementary set and the set of all squares occupied by a white pawn, we have the isolated queen pawn on d4.

    The isolated pawn matching the CQL expression in the diagrammed position just happens to be an IQP. To match only those positions in which the isolated pawn is an IQP, simply extend the CQL expression to P & ~(horizontal 1 vertical 0 7 P) & d1-8, taking the intersection of the set of all isolated white pawns with the set of all squares on the d-file.


  • Discovered check
  • The position in the diagram is from a game between Fedorov and Gulko, 1999. The bishop at g8 has just moved from f7, giving discovered check. The position is matched by the CQL expression ([QRB] & ~move to . previous) attacks k. The idea behind the expression is that if an attack on the king is by discovery, it must be by some piece other than the piece that has just moved.

    The point of the CQL sub-expression ~move to . previous is to eliminate the piece just moved from consideration among the pieces that might place the king in check. In the position depicted, move to . previous gives us the square to which the last moving piece has moved, which is g8. The complement of that set eliminates g8 from consideration. The piece designator [QRB] (line pieces, of necessity) gives us the set of squares as highlighted in the diagram, and the intersection of that set with the complementary set ([QRB] & ~move to . previous) gives us the set of highlighted squares minus g8. If any of the pieces occupying the squares of that set attack the king, then we have our discovered check — in this case by the rook at h7. In fact, the attack filter returns a set with one member, namely [h7].

    Note that the CQL expression will also match positions in which the king is in double check.


  • Attack of the pawns
  • The position in the diagram is from a game between Gunsberg and Chigorin, 1890. The white pawn at c5 has just moved from c4. The position is matched by the CQL expression ([rbn] & . attackedby P) >= 3. The set designated by [rbn] is depicted in red and brown, the set yielded by the attack filter . attackedby P is depicted in salmon and brown, and the set at the intersection is depicted in brown. A lower bound is stipulated on the cardinality of the set at the intersection.

    Note that the CQL expressions ([rbn] attackedby P) >= 3 and ([rbn] & (horizontal 1 up 1 P)) >= 3 give the same results. However, the expression (P attacks [rbn]) >= 3 does not necessarily give the same result as it gives (effectively) the number of white pawns attacking a minor piece rather than the number of minor pieces attacked by a white pawn. For example, one could have two pieces attacked by three pawns.


  • King on the line
  • The position in the diagram is from a game between Taimanov and Rukavina, 1973. Every white line piece has the opposing king on its line, with the line unobstructed by any friendly pawn. The CQL query below matches the position through a combination of subset filters and set theoretic operations.

    The direction filters yield the sets depicted in the diagram by the colored lines emanating from the black king. The anydirection filter is the equivalent of diagonal | orthogonal, the union of the two sets depicted. For each of the three in filters, the filter matches the position only because the set of every piece designated is a subset of its respective direction set.

    The first filter of the compound filter sets a lower bound on the number of white line pieces on the board by stipulating that the cardinality of the set designated is greater than some number. The last filter of the compound stipulates that there is no obstructing white pawn sitting between the line pieces and the black king. Note that the between filter yields a subset of the union of the sets depicted in the diagram. 

  • cql() 
  [QRB] > 3 
  B in diagonal k
  R in orthogonal k
  Q in anydirection k
  not P & between([QRB] k)

  • A blockaded IQP
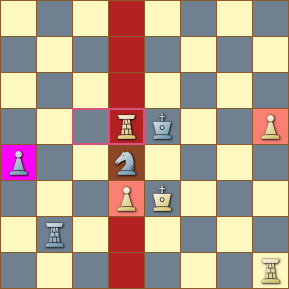  • The position in the diagram is from a game between Gelfand and Grischuk, 2011. The white rook at d5 has just made a capture from c5. The position is matched by the CQL expression n & (up 1 ((P & isolatedpawns & passedpawns) & d1-8)). (The query was further constrained by [Aa] < 10 to match positions closer to the end game.)

    The expression employs the set intersection operator four times to narrow down the matching criteria to a very specific position of interest. The sub-expression isolatedpawns & passedpawns gives us the set of highlighted pawns depicted in the diagram, each of them isolated and passed. Then the expression P & isolatedpawns & passedpawns gives us just the highlighted squares occupied by white pawns.

    We get a blockading black knight — on the set A of squares in front of (up 1) the set of squares occupied by white pawns — at the intersection of the set A and the set of all squares occupied by black knights (n & (up 1 ((P & isolatedpawns & passedpawns)))). Finally, we confine the match to blockading knights on the d-file ( & d1-8).


  • Anastasia's knight
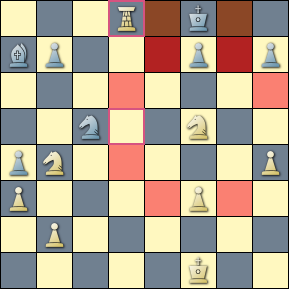  • A game between Karpov and Bareev, 1994, in which the knight guards both of the king's flight squares. Those squares are at the intersection of the king's field of attack and the knight's field of attack and the position depicted in the diagram is matched by the CQL expression {_ attackedby (N & down 3 k) & _ attackedby k} == 2.

    We must first locate the knight on a square three down from the square occupied by the king (N & down 3 k) and then take the intersection of the set of empty squares in the knight's field of attack (_ attackedby (N & down 3 k)) and the set of empty squares in the king's field of attack (_ attackedby k). The former are depicted in the diagram in salmon and red, the latter in brown and red. The intersection is depicted in red.

    Note that for the Anastasia mate pattern, both squares at the intersection must be empty. That criteria is satisfied by stipulating the cardinality of the set at exactly two. (See the example in the main document.)

    We should slow down for a moment and expand on a point about the CQL expression above that might not be intuitive for many. That expression lays out a nest of operations on eight sets, every set of which must be non-empty for the position to match. The innermost clause (N & down 3 k) must yield a non-empty set the effect of which cascades all the way out to the outermost operation (the intersection of the two fields of attack), which in turn must yield a set with exactly two members in order for the expression to match a position. Thus, if there is no white knight on the board (never mind that it must be on a precise square relative to the black king), the whole of the expression fails.


  • Boden's bishops
  • A game between Alekhine and Vasic, 1931, in which white has just sacrificed his queen on e6 drawing the king's bishop pawn away from his defense, opening the way for an atypical Boden's mate pattern. The CQL expression ((orthogonal 1 (((diagonal 1 k) & _) attackedby B)) & (((orthogonal 1 k) & _) attackedby B)) == 2 matches the position depicted in the diagram, stipulating the relative orientation of the bishops' lines of attack in the mate pattern. (See the Boden's mate example in the main document.)

    The challenge with this generalized Boden is in determining that the bishops attack along lines that are orthogonal to one another. The key in making that determination is that, if the lines are orthogonal, one bishop's line in the king's diagonal field will have its square lie adjacent to two squares in the other's line, else only one square. Those squares must be empty and are depicted in the diagram in salmon and red.

    The clauses with direction filters ((diagonal 1 k) & _) and ((orthogonal 1 k) & _) single out the empty squares in the king's field with their respective orientations. The attack filters stipulate that those squares are in the fields of attack of their respective bishops. Then (orthogonal 1 (((diagonal 1 k) & _) attackedby B)) gives us the squares e7,f6,f8,g7 in the diagram, and at the intersection of that set with (((orthogonal 1 k) & _) attackedby B) we have the set of squares depicted in salmon with cardinality of two. Thus, we know that the bishops' lines of attack are orthogonal to one another.


  • Exposing the hostile king
  • A game between Torre and Radulov, 1973, in which black has just offered his rook in an exchange sacrifice for a knight on f3, hoping to open the file in front of the king. The CQL expression reversecolor {move from (p & down 1 (k & a-h8)) capture Rook} matches the position depicted in the diagram, as the pawn does recapture in the actual game. (See the Sacrifice example in the main document.)

    Note that the reversecolor transform swaps the white/black role and flips the board. The clause (k & a-h8) places the king on the back rank. It is the pawn directly in front of the king that we want to see removed from his defense, and (p & down 1 (k & a-h8)) matches that pawn. The pawn did, in fact, recapture the rook and mate soon followed.


  • Overprotected center pawn
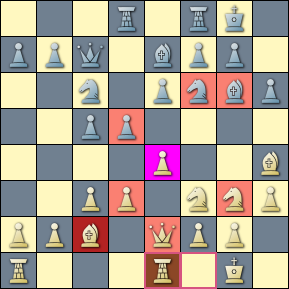  • A game between Addison and Geller, 1970, with an overprotected center pawn at e4. The CQL query below matches the position depicted in the diagram, with a lower bound set on the number of pieces defending the pawn and with the number of defenders exceeding the number of attackers. (See the corresponding example in the main document.)

    The Countem function returns the union of three sets: 1) the set of pieces directly attacking the center pawn, 2) the set of orthogonal line pieces with an xray attack on the pawn, and 3) the set of diagonal line pieces with an xray attack on the pawn through a friendly pawn. Those sets are all highlighted in the diagram for their respective sides. 

  • cql()
  function Countem(Pawn) {
    A attacks Pawn | 
    ray orthogonal (Pawn [QRBN] [QR]) |
    ray diagonal (Pawn P [QB])
  }
  piece OP in Pd-e4-5
    (Countem(OP) > 4) > {reversecolor Countem(OP)}

  • The pawn chain
  • A game between Ponomariov and Wang, 2013. The CQL query below matches the pawn chain highlighted in the diagram with base at b2. We're searching for simple chains with a single base and a lower bound on the length of the chain. (See the pawn chain example in the main document.)

    The assignment to the Chained variable captures the set of all squares occupied by a white pawn that is supported by another pawn. The set of squares given by the clause (northeast 1 P | northwest 1 P) is depicted in the diagram in salmon and red, and represents all squares on the board attacked by a white pawn (yes, we could have used an attack filter instead). Then P & (northeast 1 P | northwest 1 P) gives us the intersection of that set with the set of all white pawns on the board, depicted in red.

    The base pawns are identified as those white pawns not a member of the set of Chained pawns that support some member of the set of Chained pawns. The clause (P & ~Chained) satisfies the former condition and then (P & ~Chained) attacks Chained satisfies the whole. The base pawns are highlighted in brown in the diagram.

    We iterate over each of the base pawns looking for a chain anchored to that base and having a minimum length. The assignment to the Chain variable (Chained & (northeast Base | northwest Base)) captures the set of all squares occupied by a white pawn that is a member of the Chained set and that is also on a diagonal emanating from the base pawn. So long as there is nothing other than white pawns between the base pawn and every other pawn that is a member of Chain (not ((~P) & between(Base Chain))), we have our contiguous chain.

    The chain depicted in the diagram with base at b2 has length of four, excluding the base pawn, the rook pawn having just moved to a3. 

  • cql()
  Chained = P & (northeast 1 P | northwest 1 P)
  piece Base in (P & ~Chained) attacks Chained {
    Chain = Chained & (northeast Base | northwest Base)
    not ((~P) & between(Base Chain))
    Chain > 3
  }

  • Self-interference
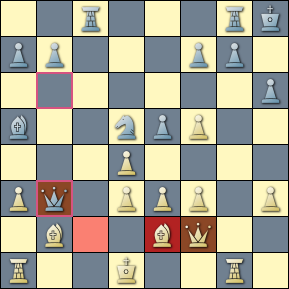  • A game between Short and Caruana, 2013, in which white has just interfered with the defense of its own king against mate. The concluding moves are ... 25. Qf2 Qb6 26. Be2 Qb3#. The CQL expression Mater =? a attacks K ray(Q parent:{move to . from ~K previous} position positionid-2:{between(Mater K) attackedby Q}) matches the position depicted in the diagram.

    We're looking for a sequence of positions whose overlap produces an intersection of two lines, one of which has been interposed such that the other may not be interposed. We employ the ray filter to determine that three critical squares are arranged along a line in the terminal position. The first is the square occupied by a defending queen which might have interposed an attack on her king. The second is the square occupied by an interfering bishop. And the third is the square on which the defending queen might have interposed the attack but for the interfering piece.

    We acquire the square occupied by the attacking piece in the terminal position with the expression Mater =? a attacks K. Then the expression position positionid-2:{between(Mater K) attackedby Q} gives us the square on which the defending piece might have interposed (depicted in salmon), looking back two positions. Finally, we have the square occupied by the interfering piece with the expression parent:{move to . from ~K previous}.


  • Example template
  • Explanation...

  • Example template
  • Explanation...

  • Example template
  • Explanation...

  • Example template
  • Explanation...

  • Example template
  • Explanation...

See also

Credits

This document is Copyright (c) 2019-2024 Lionel Hampton. The Chess Query Language was originally developed by Gady Costeff and Lewis Stiller. The upstream Scid vs PC project is managed by Steven Atkinson.

The diagrams appearing in this document were created with the Scid vs PC application's board setup dialog and comment editor. The piece set is included with that application and is credited on the project's site.

Content